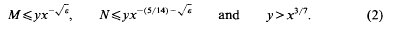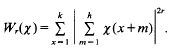Refine listing
Actions for selected content:
140 results in 11Lxx
EXPONENTIAL AND CHARACTER SUMS WITH MERSENNE NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 26 April 2012, pp. 1-13
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
EXPONENTIAL SUMS OVER POINTS OF ELLIPTIC CURVES WITH RECIPROCALS OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 13 July 2011, pp. 21-33
- Print publication:
- January 2012
-
- Article
- Export citation
DISTANCE BETWEEN ARITHMETIC PROGRESSIONS AND PERFECT SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 41-49
- Print publication:
- January 2011
-
- Article
- Export citation
One level density of low-lying zeros of families of L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 1-18
- Print publication:
- January 2011
-
- Article
-
- You have access
- Export citation
Subconvexity for a double Dirichlet series
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 2 / March 2011
- Published online by Cambridge University Press:
- 07 September 2010, pp. 355-374
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
On quadratic fields generated by the Shanks sequence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 3 / October 2009
- Published online by Cambridge University Press:
- 23 September 2009, pp. 719-729
-
- Article
-
- You have access
- Export citation
CODES ASSOCIATED WITH Sp(4,q) AND EVEN-POWER MOMENTS OF KLOOSTERMAN SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-435
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
ON THE GOWERS NORM OF PSEUDORANDOM BINARY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 259-271
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Explicit formulae for two-bridge knot polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-166
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
On the pseudorandomness of the signs of Kloosterman sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
An analogue of Van der Corput's A5-process for exponential sums
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 167-183
- Print publication:
- June 2002
-
- Article
- Export citation
Character sums and the series L(1, χ)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Character sums with exponential functions
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 75-85
- Print publication:
- December 2000
-
- Article
- Export citation
On similar short sums
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 193-204
- Print publication:
- June 1999
-
- Article
- Export citation
P-régularité de sommes d'exponentielles
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 1 / June 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-175
- Print publication:
- June 1998
-
- Article
- Export citation
A mean value theorem for exponential sums
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-307
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
A special triple exponential sum
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 137-143
- Print publication:
- June 1995
-
- Article
- Export citation
Mean values of character sums III
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-136
- Print publication:
- June 1995
-
- Article
- Export citation
On exponential sums over prime numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-437
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
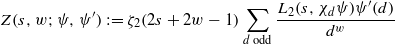
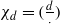 and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to
and the subscript 2 denotes the fact that the Euler factor at 2 has been removed. These double Dirichlet series can be extended to 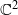 possessing a group of functional equations isomorphic to
possessing a group of functional equations isomorphic to 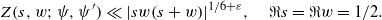
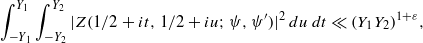
 -unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among
-unit equations as well as bounds for character sums to obtain a lower bound on the number of distinct fields among 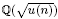 for
for 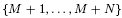 . Fields of this type include the Shanks fields and their generalizations.
. Fields of this type include the Shanks fields and their generalizations.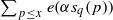 (where the sum is restricted to
(where the sum is restricted to 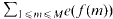 . The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].
. The saving has now to be taken to the exponent 1/20 instead of 1/32. Our main application is a “ninth derivative test” for exponential sums which is essential for giving new exponent pairs in [3].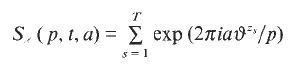
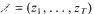 a sequence such that
a sequence such that 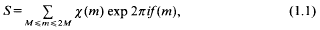
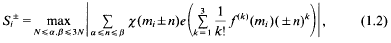

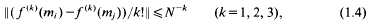
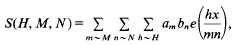
 ,
,