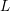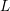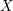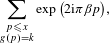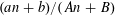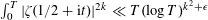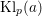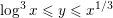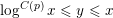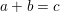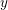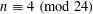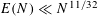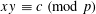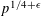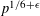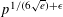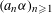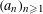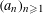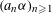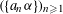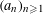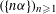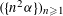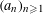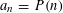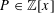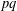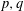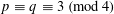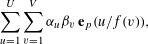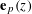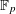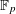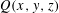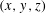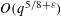Refine listing
Actions for selected content:
140 results in 11Lxx
Low-lying zeros of quadratic Dirichlet
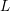 $L$ -functions: lower order terms for extended support
$L$ -functions: lower order terms for extended support
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1196-1216
- Print publication:
- June 2017
-
- Article
- Export citation
PROPRIÉTÉS LOCALES DES CHIFFRES DES NOMBRES PREMIERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 04 April 2017, pp. 189-224
- Print publication:
- January 2019
-
- Article
- Export citation
FRACTIONAL PARTS OF POLYNOMIALS OVER THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 715-733
- Print publication:
- 2017
-
- Article
- Export citation
VINOGRADOV SYSTEMS WITH A SLICE OFF
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 797-817
- Print publication:
- 2017
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME MULTIPLE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 553-560
- Print publication:
- 2017
-
- Article
- Export citation
HARMONIC ANALYSIS ON THE POSITIVE RATIONALS. DETERMINATION OF THE GROUP GENERATED BY THE RATIOS
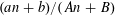 $(an+b)/(An+B)$
$(an+b)/(An+B)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 919-943
- Print publication:
- 2017
-
- Article
- Export citation
APPROXIMATING THE MAIN CONJECTURE IN VINOGRADOV’S MEAN VALUE THEOREM
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 21 December 2016, pp. 292-350
- Print publication:
- 2017
-
- Article
- Export citation
SHIFTED MOMENTS OF
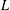 $L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
$L$ -FUNCTIONS ANDMOMENTS OF THETA FUNCTIONS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 27 September 2016, pp. 196-212
- Print publication:
- 2017
-
- Article
- Export citation
RESTRICTED SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 26 July 2016, pp. 34-52
- Print publication:
- 2017
-
- Article
- Export citation
On Euler's function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 769-775
- Print publication:
- August 2016
-
- Article
- Export citation
Kloosterman paths and the shape of exponential sums
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 7 / July 2016
- Published online by Cambridge University Press:
- 15 April 2016, pp. 1489-1516
- Print publication:
- July 2016
-
- Article
- Export citation
Minor arcs, mean values, and restriction theory for exponential sums over smooth numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 6 / June 2016
- Published online by Cambridge University Press:
- 23 February 2016, pp. 1121-1158
- Print publication:
- June 2016
-
- Article
- Export citation
ON SUMS OF FOUR SQUARES OF PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 348-361
- Print publication:
- 2016
-
- Article
- Export citation
SHORTEST DISTANCE IN MODULAR HYPERBOLA AND LEAST QUADRATIC NON-RESIDUE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 10 May 2016, pp. 860-865
- Print publication:
- 2016
-
- Article
- Export citation
METRIC RESULTS ON THE DISCREPANCY OF SEQUENCES
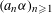 $(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES
$(a_{n}{\it\alpha})_{n\geqslant 1}$ MODULO ONE FOR INTEGER SEQUENCES 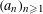 $(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
$(a_{n})_{n\geqslant 1}$ OF POLYNOMIAL GROWTH
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 05 February 2016, pp. 478-491
- Print publication:
- 2016
-
- Article
- Export citation
WARING’S PROBLEM WITH PIATETSKI-SHAPIRO NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 524-550
- Print publication:
- 2016
-
- Article
- Export citation
BIG BIASES AMONGST PRODUCTS OF TWO PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 502-507
- Print publication:
- 2016
-
- Article
- Export citation
ON BILINEAR EXPONENTIAL AND CHARACTER SUMS WITH RECIPROCALS OF POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 16 May 2016, pp. 842-859
- Print publication:
- 2016
-
- Article
- Export citation
SMALL SOLUTIONS OF QUADRATIC CONGRUENCES, AND CHARACTER SUMS WITH BINARY QUADRATIC FORMS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 18 February 2016, pp. 551-571
- Print publication:
- 2016
-
- Article
- Export citation
OPPOSITE-SIGN KLOOSTERMAN SUM ZETA FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 28 January 2016, pp. 406-429
- Print publication:
- 2016
-
- Article
- Export citation