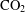Refine listing
Actions for selected content:
243 results in 65Mxx
Numerical Analysis of Inverse Elasticity Problemwith Signorini's Condition
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1045-1070
- Print publication:
- October 2016
-
- Article
- Export citation
On a Large Time-Stepping Method for the Swift-Hohenberg Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 992-1003
- Print publication:
- December 2016
-
- Article
- Export citation
Moving Finite Element Methods for a System of Semi-Linear Fractional Diffusion Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 911-931
- Print publication:
- December 2016
-
- Article
- Export citation
Numerical Analysis of the Mixed 4th-Order Runge-Kutta Scheme of Conditional Nonlinear Optimal Perturbation Approach for the EI Niño-Southern Oscillation Model
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 1023-1035
- Print publication:
- December 2016
-
- Article
- Export citation
Stability Analysis of a Fully Coupled Implicit Scheme for Inviscid Chemical Non-Equilibrium Flows
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 19 September 2016, pp. 953-970
- Print publication:
- December 2016
-
- Article
- Export citation
A Contact Line Dynamic Model for a Conducting Water Drop on an Electrowetting Device
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 811-834
- Print publication:
- September 2016
-
- Article
- Export citation
Towards a Unified Macroscopic Description of Exciton Diffusion in Organic Semiconductors
- Part of
- Probabilistic methods, simulation and stochastic differential equations
- Stochastic processes
- Partial differential equations, boundary value problems
- Equations of mathematical physics and other areas of application
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- Chemistry
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 754-772
- Print publication:
- September 2016
-
- Article
- Export citation
Efficient Semi-Lagrangian Vlasov-Maxwell Simulations of High Order Harmonic Generation from Relativistic Laser-Plasma Interactions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 31 August 2016, pp. 583-602
- Print publication:
- September 2016
-
- Article
- Export citation
DEVELOPMENT OF A PROCESS MODEL FOR THE PREDICTION OF ABSORBENT DEGRADATION DURING
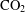 $\text{CO}_{2}$ CAPTURE
$\text{CO}_{2}$ CAPTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, pp. 339-340
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
On the Stability and CPU Time of the Implicit Runge-Kutta Schemes for Steady State Simulations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 486-511
- Print publication:
- August 2016
-
- Article
- Export citation
Numerical Solution to the Multi-Term Time Fractional Diffusion Equation in a Finite Domain
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-357
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Jacobi Spectral Collocation Method for the Time Variable-Order Fractional Mobile-Immobile Advection-Dispersion Solute Transport Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 337-352
- Print publication:
- August 2016
-
- Article
- Export citation
Mesh Spacing Estimates and Efficiency Considerations for Moving Mesh Systems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 432-450
- Print publication:
- August 2016
-
- Article
- Export citation
Modeling and Computation of CO2 Allowance Derivatives Under Jump-Diffusion Processes
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 827-846
- Print publication:
- October 2016
-
- Article
- Export citation
Identification of Elastic Orthotropic Material Parameters by the Singular Boundary Method
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 08 July 2016, pp. 810-826
- Print publication:
- October 2016
-
- Article
- Export citation
An All-Regime Lagrange-Projection Like Scheme for the Gas Dynamics Equations on Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 188-233
- Print publication:
- July 2016
-
- Article
- Export citation
The Kinematic Effects of the Defects in Liquid Crystal Dynamics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 234-249
- Print publication:
- July 2016
-
- Article
- Export citation
A Time-Space Adaptive Method for the Schrödinger Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 60-85
- Print publication:
- July 2016
-
- Article
- Export citation
Construction and Analysis of an Adapted Spectral Finite Element Method to Convective Acoustic Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 1-22
- Print publication:
- July 2016
-
- Article
- Export citation
A Posteriori Error Estimates for Conservative Local Discontinuous GalerkinMethods for the Generalized Korteweg-de Vries Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 22 June 2016, pp. 250-278
- Print publication:
- July 2016
-
- Article
- Export citation