Refine listing
Actions for selected content:
243 results in 65Mxx
Fast Simulation of Lipid Vesicle Deformation Using Spherical Harmonic Approximation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 40-64
- Print publication:
- January 2017
-
- Article
- Export citation
A Conservative Parallel Iteration Scheme for Nonlinear Diffusion Equations on Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1405-1423
- Print publication:
- November 2016
-
- Article
- Export citation
The Gradient Superconvergence of Bilinear Finite Volume Element for Elliptic Problems
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 579-594
- Print publication:
- November 2016
-
- Article
- Export citation
Mechanics-Based Solution Verification for Porous Media Models
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1127-1162
- Print publication:
- November 2016
-
- Article
- Export citation
Finite Element Simulations with Adaptively Moving Mesh for the Reaction Diffusion System
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 9 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 17 November 2016, pp. 686-704
- Print publication:
- November 2016
-
- Article
- Export citation
An Energy-Preserving Wavelet Collocation Method for General Multi-Symplectic Formulations of Hamiltonian PDEs
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1313-1339
- Print publication:
- November 2016
-
- Article
- Export citation
Exponentially accurate Hamiltonian embeddings of symplectic A-stable Runge–Kutta methods for Hamiltonian semilinear evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1265-1301
- Print publication:
- December 2016
-
- Article
- Export citation
An AMG Preconditioner for Solving the Navier-Stokes Equations with a Moving Mesh Finite Element Method
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 353-366
- Print publication:
- November 2016
-
- Article
- Export citation
A Fully Discrete Spectral Method for Fisher’s Equation on the Whole Line
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 6 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 19 October 2016, pp. 400-415
- Print publication:
- November 2016
-
- Article
- Export citation
Nonconforming Finite Element Method for the Transmission Eigenvalue Problem
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 92-103
- Print publication:
- February 2017
-
- Article
- Export citation
Runge-Kutta Discontinuous Galerkin Method with Front Tracking Method for Solving the Compressible Two-Medium Flow on Unstructured Meshes
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 73-91
- Print publication:
- February 2017
-
- Article
- Export citation
A Simple Implementation of the Semi-Lagrangian Level-Set Method
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 104-124
- Print publication:
- February 2017
-
- Article
- Export citation
XFEM for Fracture Analysis in 2D Anisotropic Elasticity
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 125-143
- Print publication:
- February 2017
-
- Article
- Export citation
Efficient and Stable Exponential Runge-Kutta Methods for Parabolic Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 157-172
- Print publication:
- February 2017
-
- Article
- Export citation
High Order Fixed-Point Sweeping WENO Methods for Steady State of Hyperbolic Conservation Laws and Its Convergence Study
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 835-869
- Print publication:
- October 2016
-
- Article
- Export citation
Two-Size Moment Multi-Fluid Model: A Robust and High-Fidelity Description of Polydisperse Moderately Dense Evaporating Sprays
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 902-943
- Print publication:
- October 2016
-
- Article
- Export citation
Hybrid and Multiplicative Overlapping Schwarz Algorithms with Standard Coarse Spaces for Mixed Linear Elasticity and Stokes Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 989-1015
- Print publication:
- October 2016
-
- Article
- Export citation
A Comparative Study of Rosenbrock-Type and Implicit Runge-Kutta Time Integration for Discontinuous Galerkin Method for Unsteady 3D Compressible Navier-Stokes equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1016-1044
- Print publication:
- October 2016
-
- Article
- Export citation
Godunov-Type Numerical Methods for a Model of Granular Flow on Open Tables with Walls
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 1071-1105
- Print publication:
- October 2016
-
- Article
- Export citation
Scale Transitions in Magnetisation Dynamics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 4 / October 2016
- Published online by Cambridge University Press:
- 05 October 2016, pp. 969-988
- Print publication:
- October 2016
-
- Article
- Export citation
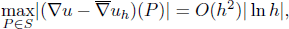
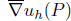 denotes the average gradient on elements containing point
denotes the average gradient on elements containing point 