Refine listing
Actions for selected content:
243 results in 65Mxx
A Third Order Adaptive ADER Scheme for One Dimensional Conservation Laws
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 829-851
- Print publication:
- September 2017
-
- Article
- Export citation
Constrained Interpolation Profile Conservative Semi-Lagrangian Scheme Based on Third-Order Polynomial Functions and Essentially Non-Oscillatory (CIP-CSL3ENO) Scheme
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 765-788
- Print publication:
- September 2017
-
- Article
- Export citation
A generalized scheme based on shifted Jacobi polynomials for numerical simulation of coupled systems of multi-term fractional-order partial differential equations
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 20 / Issue 1 / 2017
- Published online by Cambridge University Press:
- 01 July 2017, pp. 11-29
-
- Article
-
- You have access
- Export citation
Exponential Time Differencing Gauge Method for Incompressible Viscous Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 517-541
- Print publication:
- August 2017
-
- Article
- Export citation
Precorrected-FFT Accelerated Singular Boundary Method for Large-Scale Three-Dimensional Potential Problems
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 460-472
- Print publication:
- August 2017
-
- Article
- Export citation
A Symmetric Direct Discontinuous Galerkin Method for the Compressible Navier-Stokes Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 375-392
- Print publication:
- August 2017
-
- Article
- Export citation
Variations on Hermite Methods for Wave Propagation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 303-337
- Print publication:
- August 2017
-
- Article
- Export citation
On 16th and 32th Order Multioperators-Based Schemes for Smooth and Discontinuous Fluid Dynamics Solutions
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 572-598
- Print publication:
- August 2017
-
- Article
- Export citation
An Unconditionally Stable and High-Order Convergent Difference Scheme for Stokes’ First Problem for a Heated Generalized Second Grade Fluid with Fractional Derivative
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 597-613
- Print publication:
- August 2017
-
- Article
- Export citation
Fully Discrete Galerkin Finite Element Method for the Cubic Nonlinear Schrödinger Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 671-688
- Print publication:
- August 2017
-
- Article
- Export citation
Stability of Finite Difference Schemes for Hyperbolic Initial Boundary Value Problems: Numerical Boundary Layers
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 489-519
- Print publication:
- August 2017
-
- Article
- Export citation
A Numerical Approximation Structured by Mixed Finite Element and Upwind Fractional Step Difference for Semiconductor Device with Heat Conduction and Its Numerical Analysis
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 541-561
- Print publication:
- August 2017
-
- Article
- Export citation
Spectral Method Approximation of Flow Optimal Control Problems with H 1-Norm State Constraint
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 20 June 2017, pp. 614-638
- Print publication:
- August 2017
-
- Article
- Export citation
Efficient Numerical Solution of Dynamical Ginzburg-Landau Equations under the Lorentz Gauge
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 182-201
- Print publication:
- July 2017
-
- Article
- Export citation
Further Study on Errors in Metric Evaluation by Linear Upwind Schemes with Flux Splitting in Stationary Grids
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 64-94
- Print publication:
- July 2017
-
- Article
- Export citation
Implicit Asymptotic Preserving Method for Linear Transport Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 157-181
- Print publication:
- July 2017
-
- Article
- Export citation
Characteristic Local Discontinuous Galerkin Methods for Incompressible Navier-Stokes Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 202-227
- Print publication:
- July 2017
-
- Article
- Export citation
Lagrangian Mesh Model with Regridding for Planar Poiseuille Flow
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 1 / July 2017
- Published online by Cambridge University Press:
- 03 May 2017, pp. 112-132
- Print publication:
- July 2017
-
- Article
- Export citation
Computing Residual Diffusivity by Adaptive Basis Learning via Spectral Method
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 351-372
- Print publication:
- May 2017
-
- Article
- Export citation
Runge-Kutta Discontinuous Local Evolution Galerkin Methods for the Shallow Water Equations on the Cubed-Sphere Grid
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 373-419
- Print publication:
- May 2017
-
- Article
- Export citation
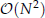 computational complexity, where
computational complexity, where 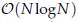 . Several numerical examples are presented to validate the developed PFFT accelerated SBM (PFFT-SBM) scheme, and the results are compared with those of the SBM without the PFFT and the analytical solutions. It is clearly found that the present PFFT-SBM is very efficient and suitable for 3D large-scale potential problems.
. Several numerical examples are presented to validate the developed PFFT accelerated SBM (PFFT-SBM) scheme, and the results are compared with those of the SBM without the PFFT and the analytical solutions. It is clearly found that the present PFFT-SBM is very efficient and suitable for 3D large-scale potential problems.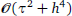 in maximum norm, where
in maximum norm, where 