This article deals with numerical inversion for the initial distribution in the multi-term time-fractional diffusion equation using final observations. The inversion problem is of instability, but it is uniquely solvable based on the solution's expression for the forward problem and estimation to the multivariate Mittag-Leffler function. From view point of optimality, solving the inversion problem is transformed to minimizing a cost functional, and existence of a minimum is proved by the weakly lower semi-continuity of the functional. Furthermore, the homotopy regularization algorithm is introduced based on the minimization problem to perform numerical inversions, and the inversion solutions with noisy data give good approximations to the exact initial distribution demonstrating the efficiency of the inversion algorithm.

In this work, we examine the mathematical analysis and numerical simulation of pattern formation in a subdiffusive multicomponents fractional-reaction-diffusion system that models the spatial interrelationship between two preys and predator species. The major result is centered on the analysis of the system for linear stability. Analysis of the main model reflects that the dynamical system is locally and globally asymptotically stable. We propose some useful theorems based on the existence and permanence of the species to validate our theoretical findings. Reliable and efficient methods in space and time are formulated to handle any space fractional reaction-diffusion system. We numerically present the complexity of the dynamics that are theoretically discussed. The simulation results in one, two and three dimensions show some amazing scenarios.

A two-layer non-hydrostatic numerical model is proposed to simulate the formation of undular bores by tsunami wave fission. These phenomena could not be produced by a hydrostatic model. Here, we derived a modified Shallow Water Equations with involving hydrodynamic pressure using two layer approach. Staggered finite volume method with predictor corrector step is applied to solve the equation numerically. Numerical dispersion relation is derived from our model to confirm the exact linear dispersion relation for dispersive waves. To illustrate the performance of our non-hydrostatic scheme in case of linear wave dispersion and non-linearity, four test cases of free surface flows are provided. The first test case is standing wave in a closed basin, which test the ability of the numerical scheme in simulating dispersive wave motion with the correct frequency. The second test case is the solitary wave propagation as the examination of owing balance between dispersion and nonlinearity. Regular wave propagation over a submerged bar test by Beji is simulated to show that our non-hydrostatic scheme described well the shoaling process as well as the linear dispersion compared with the experimental data. The last test case is the undular bore propagation.

Moving mesh methods provide an efficient way of solving partial differential equations for which large, localised variations in the solution necessitate locally dense spatial meshes. In one-dimension, meshes are typically specified using the arclength mesh density function. This choice is well-justified for piecewise polynomial interpolants, but it is only justified for spectral methods when model solutions include localised steep gradients. In this paper, one-dimensional mesh density functions are presented which are based on a spatially localised measure of the bandwidth of the approximated model solution. In considering bandwidth, these mesh density functions are well-justified for spectral methods, but are not strictly tied to the error properties of any particular spatial interpolant, and are hence widely applicable. The bandwidth mesh density functions are illustrated in two ways. First, by applying them to Chebyshev polynomial approximation of two test functions, and second, through use in periodic spectral and finite-difference moving mesh methods applied to a number of model problems in acoustics. These problems include a heterogeneous advection equation, the viscous Burgers’ equation, and the Korteweg-de Vries equation. Simulation results demonstrate solution convergence rates that are up to an order of magnitude faster using the bandwidth mesh density functions than uniform meshes, and around three times faster than those using the arclength mesh density function.

We describe a numerical model to simulate the non-linear elasto-plastic dynamics of compressible materials. The model is fully Eulerian and it is discretized on a fixed Cartesian mesh. The hyperelastic constitutive law considered is neohookean and the plasticity model is based on a multiplicative decomposition of the inverse deformation tensor. The model is thermodynamically consistent and it is shown to be stable in the sense that the norm of the deviatoric stress tensor beyond yield is non increasing. The multimaterial integration scheme is based on a simple numerical flux function that keeps the interfaces sharp. Numerical illustrations in one to three space dimensions of high-speed multimaterial impacts in air are presented.

This paper proposes a novel distance derivative weighted ENO (DDWENO) limiter based on fixed reconstruction stencil and applies it to the second- and highorder finite volume method on unstructured grids. We choose the standard deviation coefficients of the flow variables as the smooth indicators by using the k-exact reconstruction method, and obtain the limited derivatives of the flow variables by weighting all derivatives of each cell according to smoothness. Furthermore, an additional weighting coefficient related to distance is introduced to emphasize the contribution of the central cell in smooth regions. The developed limiter, combining the advantages of the slope limiters and WENO-type limiters, can achieve the similar effect of WENO schemes in the fixed stencil with high computational efficiency. The numerical cases demonstrate that the DDWENO limiter can preserve the numerical accuracy in smooth regions, and capture the shock waves clearly and steeply as well.

This paper presents topology optimization of capillary, the typical two-phase flow with immiscible fluids, where the level set method and diffuse-interface model are combined to implement the proposed method. The two-phase flow is described by the diffuse-interface model with essential no slip condition imposed on the wall, where the singularity at the contact line is regularized by the molecular diffusion at the interface between two immiscible fluids. The level set method is utilized to express the fluid and solid phases in the flows and the wall energy at the implicit fluid-solid interface. Based on the variational procedure for the total free energy of two-phase flow, the Cahn-Hilliard equations for the diffuse-interface model are modified for the two-phase flow with implicit boundary expressed by the level set method. Then the topology optimization problem for the two-phase flow is constructed for the cost functional with general formulation. The sensitivity analysis is implemented by using the continuous adjoint method. The level set function is evolved by solving the Hamilton-Jacobian equation, and numerical test is carried out for capillary to demonstrate the robustness of the proposed topology optimization method. It is straightforward to extend this proposed method into the other two-phase flows with two immiscible fluids.

Anisotropic mesh adaptation is studied for linear finite element solution of 3D anisotropic diffusion problems. The 𝕄-uniform mesh approach is used, where an anisotropic adaptive mesh is generated as a uniform one in the metric specified by a tensor. In addition to mesh adaptation, preservation of the maximum principle is also studied. Some new sufficient conditions for maximum principle preservation are developed, and a mesh quality measure is defined to server as a good indicator. Four different metric tensors are investigated: one is the identity matrix, one focuses on minimizing an error bound, another one on preservation of the maximum principle, while the fourth combines both. Numerical examples show that these metric tensors serve their purposes. Particularly, the fourth leads to meshes that improve the satisfaction of the maximum principle by the finite element solution while concentrating elements in regions where the error is large. Application of the anisotropic mesh adaptation to fractured reservoir simulation in petroleum engineering is also investigated, where unphysical solutions can occur and mesh adaptation can help improving the satisfaction of the maximum principle.

A numerical time-stepping algorithm for differential or partial differential equations is proposed that adaptively modifies the dimensionality of the underlying modal basis expansion. Specifically, the method takes advantage of any underlying low-dimensional manifolds or subspaces in the system by using dimensionality-reduction techniques, such as the proper orthogonal decomposition, in order to adaptively represent the solution in the optimal basis modes. The method can provide significant computational savings for systems where low-dimensional manifolds are present since the reduction can lower the dimensionality of the underlying high-dimensional system by orders of magnitude. A comparison of the computational efficiency and error for this method are given showing the algorithm to be potentially of great value for high-dimensional dynamical systems simulations, especially where slow-manifold dynamics are known to arise. The method is envisioned to automatically take advantage of any potential computational saving associated with dimensionality-reduction, much as adaptive time-steppers automatically take advantage of large step sizes whenever possible.

The pricing model for American lookback options can be characterised as a two-dimensional free boundary problem. The main challenge in this problem is the free boundary, which is also the main concern for financial investors. We use a standard technique to reduce the pricing model to a one-dimensional linear complementarity problem on a bounded domain and obtain a corresponding variational inequality. The inequality is discretised by finite differences and finite elements in the temporal and spatial directions, respectively. By enforcing inequality constraints related to the options using Lagrange multipliers, the discretised variational inequality is reformulated as a set of semi-smooth equations, which are solved by a primal-dual active set method. One of the major advantages of our algorithm is that we can obtain the option values and the free boundary simultaneously, and numerical simulations show that our approach is as efficient as some other methods.

The numerical solution of the time-fractional sub-diffusion equation on an unbounded domain in two-dimensional space is considered, where a circular artificial boundary is introduced to divide the unbounded domain into a bounded computational domain and an unbounded exterior domain. The local artificial boundary conditions for the fractional sub-diffusion equation are designed on the circular artificial boundary by a joint Laplace transform and Fourier series expansion, and some auxiliary variables are introduced to circumvent high-order derivatives in the artificial boundary conditions. The original problem defined on the unbounded domain is thus reduced to an initial boundary value problem on a bounded computational domain. A finite difference and L1 approximation are applied for the space variables and the Caputo time-fractional derivative, respectively. Two numerical examples demonstrate the performance of the proposed method.

We present a moving-least-square immersed boundary method for solving viscous incompressible flow involving deformable and rigid boundaries on a uniform Cartesian grid. For rigid boundaries, noslip conditions at the rigid interfaces are enforced using the immersed-boundary direct-forcing method. We propose a reconstruction approach that utilizes moving least squares (MLS) method to reconstruct the velocity at the forcing points in the vicinity of the rigid boundaries. For deformable boundaries, MLS method is employed to construct the interpolation and distribution operators for the immersed boundary points in the vicinity of the rigid boundaries instead of using discrete delta functions. The MLS approach allows us to avoid distributing the Lagrangian forces into the solid domains as well as to avoid using the velocity of points inside the solid domains to compute the velocity of the deformable boundaries. The present numerical technique has been validated by several examples including a Poiseuille flow in a tube, deformations of elastic capsules in shear flow and dynamics of red-blood cell in microfluidic devices.

In this work, we introduce an IMEX discontinuous Galerkin solver for the weakly compressible isentropic Euler equations. The splitting needed for the IMEX temporal integration is based on the recently introduced reference solution splitting [32, 52], which makes use of the incompressible solution. We show that the overall method is asymptotic preserving. Numerical results show the performance of the algorithm which is stable under a convective CFL condition and does not show any order degradation.

An adaptive moving mesh finite difference method is presented to solve two types of equations with dynamic capillary pressure effect in porous media. One is the non-equilibrium Richards Equation and the other is the modified Buckley-Leverett equation. The governing equations are discretized with an adaptive moving mesh finite difference method in the space direction and an implicit-explicit method in the time direction. In order to obtain high quality meshes, an adaptive monitor function with directional control is applied to redistribute the mesh grid in every time step, then a diffusive mechanism is used to smooth the monitor function. The behaviors of the central difference flux, the standard local Lax-Friedrich flux and the local Lax-Friedrich flux with reconstruction are investigated by solving a 1D modified Buckley-Leverett equation. With the moving mesh technique, good mesh quality and high numerical accuracy are obtained. A collection of one-dimensional and two-dimensional numerical experiments is presented to demonstrate the accuracy and effectiveness of the proposed method.

The fractional derivatives include nonlocal information and thus their calculation requires huge storage and computational cost for long time simulations. We present an efficient and high-order accurate numerical formula to speed up the evaluation of the Caputo fractional derivative based on the L2-1σ formula proposed in [A. Alikhanov, J. Comput. Phys., 280 (2015), pp. 424-438], and employing the sum-of-exponentials approximation to the kernel function appeared in the Caputo fractional derivative. Both theoretically and numerically, we prove that while applied to solving time fractional diffusion equations, our scheme not only has unconditional stability and high accuracy but also reduces the storage and computational cost.

In this paper we are concerned with numerical methods for nonlinear time-dependent problem coupled by electron, ion and photon temperatures in two dimensions, which is called the 2D-3T heat conduction equations. We propose discontinuous Galerkin (DG) methods for the discretization of the equations. For solving the resulting discrete system, we employ two domain decomposition (DD) preconditioners, one of which is associated with the non-overlapping DDM and the other is based on DDM with small overlap. The preconditioners are constructed by dropping the couplings between particles and each preconditioner consists of three preconditioners with smaller matrix size. To gauge the efficiency of the preconditioners, we test two examples and make different settings of parameters. Numerical results show that the proposed preconditioners are very effective to the 2D-3T problem.

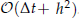We present a convex-splitting scheme for the fourth order parabolic equation derived from a diffuse interface model with Peng-Robinson equation of state for pure substance. The semi-implicit scheme is proven to be uniquely solvable, mass conservative, unconditionally energy stable and L∞ convergent with the order of . The numerical results verify the effectiveness of the proposed algorithm and also show good agreement of the numerical solution with laboratory experimental results.

In this work, element free Galerkin (EFG) method is posed for solving nonlinear, reaction-diffusion systems which are often employed in mathematical modeling in developmental biology. A predicator-corrector scheme is applied, to avoid directly solving of coupled nonlinear systems. The EFG method employs the moving least squares (MLS) approximation to construct shape functions. This method uses only a set of nodal points and a geometrical description of the body to discretize the governing equation. No mesh in the classical sense is needed. However a background mesh is used for integration purpose. Numerical solutions for two cases of interest, the Schnakenberg model and the Gierer-Meinhardt model, in various regions is presented to demonstrate the effects of various domain geometries on the resulting biological patterns.

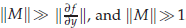This paper is devoted to an extension of the finite-energy condition for extended Runge-Kutta-Nyström (ERKN) integrators and applications to nonlinear wave equations. We begin with an error analysis for the integrators for multi-frequency highly oscillatory systems , where M is positive semi-definite, . The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix 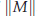M and initial conditions are based on particular spatial discretisations. Similarly to the error analysis for Gaustchi-type methods of order two, where a finite-energy condition bounding amplitudes of high oscillations is satisfied by the solution, a finite-energy condition for the semi-discretisation of nonlinear wave equations is introduced and analysed. These ensure that the error bound of ERKN methods is independent of . Since stepsizes are not restricted by frequencies of M, large stepsizes can be employed by our ERKN integrators of arbitrary high order. Numerical experiments provided in this paper have demonstrated that our results are truly promising, and consistent with our analysis and prediction.

We introduce a third order adaptive mesh method to arbitrary high order Godunov approach. Our adaptive mesh method consists of two parts, i.e., mesh-redistribution algorithm and solution algorithm. The mesh-redistribution algorithm is derived based on variational approach, while a new solution algorithm is developed to preserve high order numerical accuracy well. The feature of proposed Adaptive ADER scheme includes that 1). all simulations in this paper are stable for large CFL number, 2). third order convergence of the numerical solutions is successfully observed with adaptive mesh method, and 3). high resolution and non-oscillatory numerical solutions are obtained successfully when there are shocks in the solution. A variety of numerical examples show the feature well.