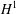Refine listing
Actions for selected content:
243 results in 65Mxx
Resonance-based schemes for dispersive equations via decorated trees
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 January 2022, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECTRALLY ACCURATE OPTION PRICING UNDER THE TIME-FRACTIONAL BLACK–SCHOLES MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 25 August 2021, pp. 228-248
-
- Article
- Export citation
LOCALIZED RADIAL BASIS FUNCTIONS FOR NO-ARBITRAGE PRICING OF OPTIONS UNDER STOCHASTIC ALPHA–BETA–RHO DYNAMICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 203-227
-
- Article
- Export citation
ANALYSIS OF CELL TRANSMISSION MODEL FOR TRAFFIC FLOW SIMULATION WITH APPLICATION TO NETWORK TRAFFIC
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 18 May 2021, pp. 84-99
-
- Article
- Export citation
SLOW-BURNING INSTABILITIES OF DUFORT–FRANKEL FINITE DIFFERENCING
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 23-38
-
- Article
- Export citation
EFFICIENT COMPUTATION OF COORDINATE-FREE MODELS OF FLAME FRONTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 58-69
-
- Article
- Export citation
Understanding rapid charge and discharge in nano-structured lithium iron phosphate cathodes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 01 March 2021, pp. 328-368
-
- Article
-
- You have access
- Open access
- Export citation
LINEARLY IMPLICIT ENERGY-PRESERVING FOURIER PSEUDOSPECTRAL SCHEMES FOR THE COMPLEX MODIFIED KORTEWEG–DE VRIES EQUATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 3 / July 2020
- Published online by Cambridge University Press:
- 12 January 2021, pp. 256-273
-
- Article
-
- You have access
- Export citation
IMPLEMENTATION OF HIGH-ORDER, DISCONTINUOUS GALERKIN TIME STEPPING FOR FRACTIONAL DIFFUSION PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 62 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 06 November 2020, pp. 121-147
-
- Article
-
- You have access
- Export citation
A Q-WADGE HIERARCHY IN QUASI-POLISH SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 05 October 2020, pp. 732-757
- Print publication:
- June 2022
-
- Article
- Export citation
A multi-level procedure for enhancing accuracy of machine learning algorithms
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 14 July 2020, pp. 436-469
-
- Article
- Export citation
A non-local traffic flow model for 1-to-1 junctions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 1029-1049
-
- Article
- Export citation
NUMERICAL ENTROPY PRODUCTION AS SMOOTHNESS INDICATOR FOR SHALLOW WATER EQUATIONS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 4 / October 2019
- Published online by Cambridge University Press:
- 28 November 2019, pp. 398-415
-
- Article
-
- You have access
- Export citation
A NEW LINEAR AND CONSERVATIVE FINITE DIFFERENCE SCHEME FOR THE GROSS–PITAEVSKII EQUATION WITH ANGULAR MOMENTUM ROTATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 08 April 2019, pp. 204-232
-
- Article
-
- You have access
- Export citation
A RAYLEIGH–RITZ METHOD FOR NAVIER–STOKES FLOW THROUGH CURVED DUCTS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 1-22
-
- Article
-
- You have access
- Export citation
Simulation of multiphase porous media flows with minimising movement and finite volume schemes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 1123-1152
-
- Article
- Export citation
A measure theoretic approach to traffic flow optimisation on networks
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 1187-1209
-
- Article
- Export citation
Displacement convexity for the entropy in semi-discrete non-linear Fokker–Planck equations
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 10 January 2018, pp. 1103-1122
-
- Article
-
- You have access
- Open access
- Export citation
An Adaptive Semi-Lagrangian Level-Set Method for Convection-Diffusion Equations on Evolving Interfaces
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1364-1382
- Print publication:
- December 2017
-
- Article
- Export citation
Nonlinear Vibrations of Two-Span Composite Laminated Plates with Equal and Unequal Subspan Lengths
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1485-1505
- Print publication:
- December 2017
-
- Article
- Export citation