Refine listing
Actions for selected content:
243 results in 65Mxx
An Efficient Implementation of the Divergence Free Constraint in a Discontinuous Galerkin Method for Magnetohydrodynamics on Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 07 February 2017, pp. 423-442
- Print publication:
- February 2017
-
- Article
- Export citation
An Efficient Numerical Method for Mean Curvature-Based Image Registration Model
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 125-142
- Print publication:
- February 2017
-
- Article
- Export citation
The Oseen Type Finite Element Iterative Method for the Stationary Incompressible Magnetohydrodynamics
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 775-794
- Print publication:
- August 2017
-
- Article
- Export citation
Numerical Simulation for the Variable-Order Fractional Schrödinger Equation with the Quantum Riesz-Feller Derivative
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 990-1011
- Print publication:
- August 2017
-
- Article
- Export citation
A Time Second-Order Mass-Conserved Implicit-Explicit Domain Decomposition Scheme for Solving the Diffusion Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 795-817
- Print publication:
- August 2017
-
- Article
- Export citation
Finite Element Solution for MHD Flow of Nanofluids with Heat and Mass Transfer through a Porous Media with Thermal Radiation, Viscous Dissipation and Chemical Reaction Effects
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 18 January 2017, pp. 904-923
- Print publication:
- August 2017
-
- Article
- Export citation
A New Two-Grid Method for Expanded Mixed Finite Element Solution of Nonlinear Reaction Diffusion Equations
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 757-774
- Print publication:
- June 2017
-
- Article
- Export citation
A Combined Discontinuous Galerkin Method for Saltwater Intrusion Problem with Splitting Mixed Procedure
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 651-666
- Print publication:
- June 2017
-
- Article
- Export citation
Moving Mesh Finite Element Method for Unsteady Navier-Stokes Flow
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 742-756
- Print publication:
- June 2017
-
- Article
- Export citation
Convergence of Monotone Schemes for Conservation Laws with Zero-Flux Boundary Conditions
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 17 January 2017, pp. 515-542
- Print publication:
- June 2017
-
- Article
- Export citation
The Motion of a Neutrally Buoyant Ellipsoid Inside Square Tube Flows
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 233-249
- Print publication:
- April 2017
-
- Article
- Export citation
Analysis of Solving Galerkin Finite Element Methods with Symmetric Pressure Stabilization for the Unsteady Navier-Stokes Equations Using Conforming Equal Order Interpolation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 362-377
- Print publication:
- April 2017
-
- Article
- Export citation
A New Family of Difference Schemes for Space Fractional Advection Diffusion Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 282-306
- Print publication:
- April 2017
-
- Article
- Export citation
New Conservative Finite Volume Element Schemes for the Modified Regularized Long Wave Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 250-271
- Print publication:
- April 2017
-
- Article
- Export citation
A High-Efficient Algorithm for Parabolic Problems with Time-Dependent Coefficients
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 501-514
- Print publication:
- April 2017
-
- Article
- Export citation
Effects of Viscous Dissipation and Radiation on MHD Natural Convection in Oblique Porous Cavity with Constant Heat Flux
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 463-484
- Print publication:
- April 2017
-
- Article
- Export citation
A-Posteriori Error Estimates for Uniform p-Version Finite Element Methods in Square
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 272-281
- Print publication:
- April 2017
-
- Article
- Export citation
Optimal Superconvergence of Energy Conserving Local Discontinuous Galerkin Methods for Wave Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 211-236
- Print publication:
- January 2017
-
- Article
- Export citation
Monotone Finite Volume Scheme for Three Dimensional Diffusion Equation on Tetrahedral Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 162-181
- Print publication:
- January 2017
-
- Article
- Export citation
High Order Accurate Direct Arbitrary-Lagrangian-Eulerian ADER-MOOD Finite Volume Schemes for Non-Conservative Hyperbolic Systems with Stiff Source Terms
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 271-312
- Print publication:
- January 2017
-
- Article
- Export citation
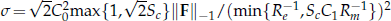
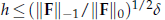 . Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.
. Finally, some numerical tests are presented to demonstrate the effectiveness of this algorithm.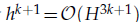 . An numerical example is also given to illustrate the effectiveness of the algorithm.
. An numerical example is also given to illustrate the effectiveness of the algorithm.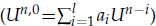 as good initial value of
as good initial value of 