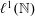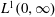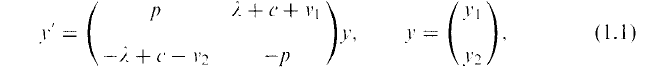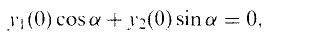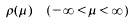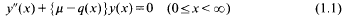Refine listing
Actions for selected content:
38 results in 34Lxx
MULTIPLICITIES OF EIGENVALUES OF THE DIFFUSION OPERATOR WITH RANDOM JUMPS FROM THE BOUNDARY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 101-113
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Partial inverse problems for Sturm–Liouville operators on trees
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 15 August 2017, pp. 917-933
- Print publication:
- October 2017
-
- Article
- Export citation
Discreteness of spectrum for Schrödinger operators with δʹ-type conditions on infinite regular trees
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1091-1117
- Print publication:
- October 2017
-
- Article
- Export citation
Geometric aspects of self-adjoint Sturm–Liouville problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1279-1295
- Print publication:
- December 2017
-
- Article
- Export citation
A Filtered-Davidson Method for Large Symmetric Eigenvalue Problems
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 21-37
- Print publication:
- February 2017
-
- Article
- Export citation
Borg's Periodicity Theorems for First-Order Self-Adjoint Systems with Complex Potentials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 19 December 2016, pp. 615-633
-
- Article
- Export citation
Spectral Curve of the Halphen Operator
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 14 November 2016, pp. 451-460
-
- Article
- Export citation
Nonconforming Finite Element Method for the Transmission Eigenvalue Problem
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 92-103
- Print publication:
- February 2017
-
- Article
- Export citation
A criterion for compactness in Lp(ℝ) of the resolvent of the maximal general form Sturm–Liouville operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 483-508
- Print publication:
- June 2016
-
- Article
- Export citation
Optimal Stopping Problems in Diffusion-Type Models with Running Maxima and Drawdowns
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 799-817
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
THE FINITE SECTION METHOD FOR DISSIPATIVE OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 415-443
- Print publication:
- July 2014
-
- Article
- Export citation
THE DISCRETENESS OF SPECTRUM FOR HIGHER-ORDER DIFFERENTIAL OPERATORS IN WEIGHTED FUNCTION SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 09 August 2012, pp. 370-376
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Spectral analysis of integro-differential operators applied in linear antenna modelling
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 333-354
-
- Article
-
- You have access
- Export citation
SINGULAR SCHRÖDINGER OPERATORS IN ONE DIMENSION
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 April 2012, pp. 141-159
- Print publication:
- January 2013
-
- Article
- Export citation
STURM–LIOUVILLE PROBLEMS WITH DISCONTINUOUS POTENTIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 485-494
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
The form of the spectral functions associated with Dirac equations
- Part of
-
- Journal:
- Mathematika / Volume 50 / Issue 1-2 / December 2003
- Published online by Cambridge University Press:
- 26 February 2010, pp. 153-165
- Print publication:
- December 2003
-
- Article
- Export citation
An extension of Henrici theorem for the joint approximate spectrum of commuting spectral operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 2 / October 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-246
- Print publication:
- October 2003
-
- Article
-
- You have access
- Export citation
On the location of spectral concentration for perturbed discrete spectra
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-154
- Print publication:
- June 1999
-
- Article
- Export citation
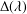
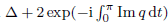 are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which
are double zeros if and only if this self-adjoint system is unitarily equivalent to one in which 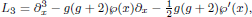
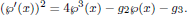
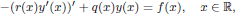
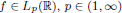 and
and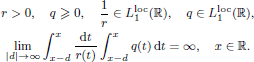
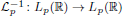 of the maximal continuously invertible Sturm–Liouville operator
of the maximal continuously invertible Sturm–Liouville operator 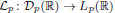 . Here
. Here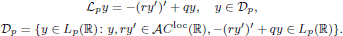
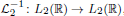 , we obtain two-sided sharp-by-order estimates of the maximal eigenvalue.
, we obtain two-sided sharp-by-order estimates of the maximal eigenvalue.