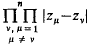Refine listing
Actions for selected content:
35 results in 31Axx
On the existence of harmonic mappings between doubly connected domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 22 April 2018, pp. 619-628
- Print publication:
- June 2018
-
- Article
- Export citation
LANDAU’S THEOREM FOR SOLUTIONS OF THE
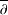 $\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 28 September 2017, pp. 80-87
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 07 August 2017, pp. 256-262
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 02 March 2017, pp. 457-466
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL EXTENSIONS OF HARMONIC MAPPINGS WITH A COMPLEX PARAMETER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 19 September 2016, pp. 307-315
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
RADII OF HARMONIC MAPPINGS IN THE PLANE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 331-347
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF FINITE CRITICAL TRAJECTORIES IN A FAMILY OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 80-91
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 92-100
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 145-157
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Supremum and infimum of subharmonic functions of order between 1 and 2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 685-693
-
- Article
-
- You have access
- Export citation
BOUNDARY BEHAVIOR OF SUPERHARMONIC FUNCTIONS SATISFYING NONLINEAR INEQUALITIES IN A PLANAR SMOOTH DOMAIN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 253-261
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
Positive Harmonic Functions and Complete Metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 286-297
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
A free boundary problem in an annulus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-181
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Dirichlet-finite outer functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-293
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
On the distribution of Fekete points II
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-49
- Print publication:
- June 1971
-
- Article
- Export citation
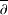
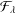
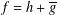
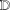

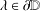
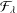

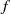
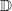
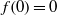
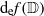
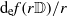
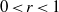
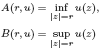
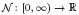 is a non-negative non-decreasing convex function of log
is a non-negative non-decreasing convex function of log 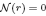 for all small
for all small 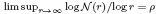 , where 1 < ρ < 2, and define
, where 1 < ρ < 2, and define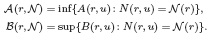
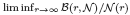 and a sharp lower bound is obtained for
and a sharp lower bound is obtained for 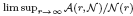 .
.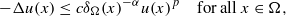
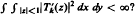 We shall show, among other results, that the answer is in the positive if
We shall show, among other results, that the answer is in the positive if 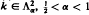 , with ess inf
, with ess inf