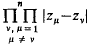Refine listing
Actions for selected content:
110 results in 31xxx
Liouville properties on graphs
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 133-148
- Print publication:
- June 1997
-
- Article
- Export citation
The parabolicity of Brelot's harmonic spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-27
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
Harmonic morphisms and conformal foliations by geodesics of three-dimensional space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 1 / August 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 118-153
- Print publication:
- August 1991
-
- Article
-
- You have access
- Export citation
The potential due to a circular parallel plate condenser
- Part of
-
- Journal:
- Mathematika / Volume 37 / Issue 2 / December 1990
- Published online by Cambridge University Press:
- 26 February 2010, pp. 217-231
- Print publication:
- December 1990
-
- Article
- Export citation
Positive Harmonic Functions and Complete Metrics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 286-297
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Growth of solutions of weakly coupled parabolic systems and Laplace's equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-403
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Thinness and boundary behaviour of potentials for the heat equation
- Part of
-
- Journal:
- Mathematika / Volume 32 / Issue 1 / June 1985
- Published online by Cambridge University Press:
- 26 February 2010, pp. 90-95
- Print publication:
- June 1985
-
- Article
- Export citation
A free boundary problem in an annulus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-181
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Dirichlet-finite outer functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-293
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
On the distribution of Fekete points II
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 40-49
- Print publication:
- June 1971
-
- Article
- Export citation
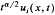 exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.
exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.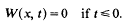
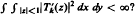 We shall show, among other results, that the answer is in the positive if
We shall show, among other results, that the answer is in the positive if 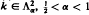 , with ess inf
, with ess inf