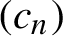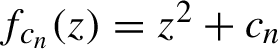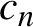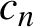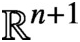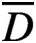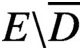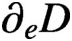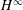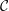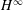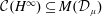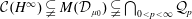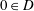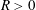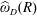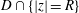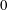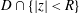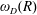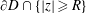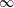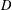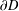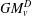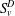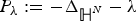Refine listing
Actions for selected content:
110 results in 31xxx
Total disconnectedness of Julia sets of random quadratic polynomials
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1764-1780
- Print publication:
- May 2022
-
- Article
- Export citation
Sharp Caffarelli–Kohn–Nirenberg inequalities on Riemannian manifolds: the influence of curvature
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 102-127
- Print publication:
- February 2022
-
- Article
- Export citation
UNIQUENESS OF EXTENDABLE TEMPERATURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 311-317
- Print publication:
- April 2021
-
- Article
- Export citation
The Lp Minkowski problem for q-capacity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 September 2020, pp. 1247-1277
- Print publication:
- August 2021
-
- Article
- Export citation
Continuity of condenser capacity under holomorphic motions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 340-348
- Print publication:
- June 2021
-
- Article
- Export citation
Edge corrections for parallel-plate capacitors
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 30 April 2020, pp. 226-241
-
- Article
-
- You have access
- Open access
- Export citation
ON THE HARMONIC ZYGMUND SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 11 March 2020, pp. 466-476
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ALGEBRAIC STRUCTURE OF THE RANGE OF A TRIGONOMETRIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 251-260
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
QUASICONFORMAL HARMONIC MAPPINGS BETWEEN DOMAINS CONTAINING INFINITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 109-117
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The Range of the Cesàro Operator Acting on
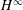 $H^{\infty }$
$H^{\infty }$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 633-642
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
On a Property of Harmonic Measure on Simply Connected Domains
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 November 2019, pp. 297-317
- Print publication:
- April 2021
-
- Article
- Export citation
BOUNDARY SCHWARZ LEMMA FOR SOLUTIONS TO NONHOMOGENEOUS BIHARMONIC EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 09 September 2019, pp. 470-478
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
New sharp Hardy and Rellich type inequalities on Cartan–Hadamard manifolds and their improvements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 2952-2981
- Print publication:
- December 2020
-
- Article
- Export citation
Equality case for an elliptic area condenser inequality and a related Schwarz type lemma
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 19 August 2019, pp. 91-104
-
- Article
- Export citation
Asymptotic Behaviour of the Energy Integral of a Two-Parameter Homogenization Problem with Nonlinear Periodic Robin Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 22 March 2019, pp. 985-1016
-
- Article
- Export citation
Bilinear forms on potential spaces in the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 19 March 2019, pp. 2117-2154
- Print publication:
- August 2020
-
- Article
- Export citation
EXTENDABLE TEMPERATURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 297-303
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
An optimal improvement for the Hardy inequality on the hyperbolic space and related manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1699-1736
- Print publication:
- August 2020
-
- Article
- Export citation
Monotonicity of non-Liouville property for positive solutions of skew product elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1429-1449
- Print publication:
- June 2020
-
- Article
- Export citation
Existence and non-existence of minimal graphic and p-harmonic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 25 January 2019, pp. 341-366
- Print publication:
- February 2020
-
- Article
- Export citation