Refine listing
Actions for selected content:
110 results in 31xxx
A Well-Conditioned Hypersingular Boundary Element Method for Electrostatic Potentials in the Presence of Inhomogeneities within Layered Media
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 12 April 2016, pp. 970-997
- Print publication:
- April 2016
-
- Article
- Export citation
ON THE EXISTENCE OF FINITE CRITICAL TRAJECTORIES IN A FAMILY OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 80-91
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF THE CLUNIE–SHEIL-SMALL THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 92-100
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
THERMIC MINORANTS AND REDUCTIONS OF SUPERTEMPERATURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 128-144
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
REGULARITY OF BOUNDARY POINTS IN THE DIRICHLET PROBLEM FOR THE HEAT EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 27 August 2014, pp. 476-485
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
COEFFICIENT ESTIMATES, LANDAU’S THEOREM AND LIPSCHITZ-TYPE SPACES ON PLANAR HARMONIC MAPPINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 198-215
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
THE
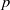 $p$-HARMONIC BOUNDARY AND
$p$-HARMONIC BOUNDARY AND 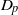 ${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
${D}_{p} $-MASSIVE SUBSETS OF A GRAPH OF BOUNDED DEGREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 149-158
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
WEAK CONTINUITY OF THE COMPLEX
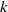 $k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
$k$-HESSIAN OPERATORS WITH RESPECT TO LOCAL UNIFORM CONVERGENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 11 June 2013, pp. 227-233
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
ASPECTS OF RECURRENCE AND TRANSIENCE FOR LÉVY PROCESSES IN TRANSFORMATION GROUPS AND NONCOMPACT RIEMANNIAN SYMMETRIC PAIRS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 31 May 2013, pp. 304-320
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
HOLOMORPHIC FUNCTIONS WITH IMAGE OF GIVEN LOGARITHMIC OR ELLIPTIC CAPACITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 145-157
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
Convergence of Brownian motion with a scaled Dirac delta potential
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 403-427
-
- Article
-
- You have access
- Export citation
TWO NONTRIVIAL WEAK SOLUTIONS FOR THE DIRICHLET PROBLEM ON THE SIERPIŃSKI GASKET
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 395-414
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
THE MEAN-VALUE PROPERTY AND (α,β)-HARMONICITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 2 / October 2011
- Published online by Cambridge University Press:
- 14 October 2011, pp. 189-206
- Print publication:
- October 2011
-
- Article
-
- You have access
- Export citation
Supremum and infimum of subharmonic functions of order between 1 and 2
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 08 April 2011, pp. 685-693
-
- Article
-
- You have access
- Export citation
BOUNDARY BEHAVIOR OF SUPERHARMONIC FUNCTIONS SATISFYING NONLINEAR INEQUALITIES IN A PLANAR SMOOTH DOMAIN
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 09 October 2009, pp. 253-261
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS IN NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 324-334
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
DISTANCE GEOMETRY IN QUASIHYPERMETRIC SPACES. I
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 19 June 2009, pp. 1-25
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
On convexity and weak closeness for the set of Φ-superharmonic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-440
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Transformation formula of higher order integrals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 155-164
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
Time-isolated Singularities of Temperatures
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 416-429
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
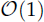 condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.
condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.
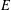

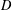
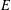


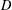
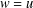
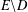
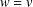
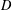
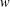
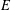
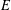
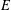
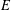
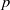
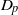
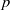
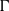
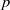
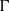
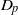
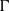

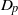
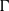
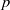
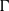

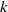
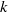
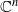
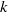
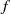
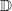
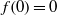
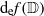
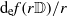
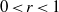
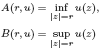
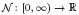 is a non-negative non-decreasing convex function of log
is a non-negative non-decreasing convex function of log 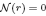 for all small
for all small 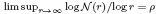 , where 1 < ρ < 2, and define
, where 1 < ρ < 2, and define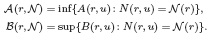
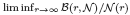 and a sharp lower bound is obtained for
and a sharp lower bound is obtained for 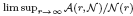 .
.