We give a direct proof of the strong maximum principle on finite dimensional RCD spaces based on the Laplacian comparison of the squared distance.

We study the heat semigroup maximal operator associated with a well-known orthonormal system in the $d$-dimensional ball. The corresponding heat kernel is shown to satisfy Gaussian bounds. As a consequence, we can prove weighted $L^{p}$ estimates, as well as some weighted inequalities in mixed norm spaces, for this maximal operator.

Utilizing frameworks developed by Delsarte, Yudin and Levenshtein, we deduce linear programming lower bounds (as $N\rightarrow \infty$) for the Riesz energy of $N$-point configurations on the $d$-dimensional unit sphere in the so-called hypersingular case; i.e., for non-integrable Riesz kernels of the form $|x-y|^{-s}$ with $s>d$. As a consequence, we immediately get (thanks to the poppy-seed bagel theorem) lower estimates for the large $N$ limits of minimal hypersingular Riesz energy on compact $d$-rectifiable sets. Furthermore, for the Gaussian potential $\exp (-\unicode[STIX]{x1D6FC}|x-y|^{2})$ on $\mathbb{R}^{p}$, we obtain lower bounds for the energy of infinite configurations having a prescribed density.

Let ${\mathcal{D}}_{\unicode[STIX]{x1D707}}$ be Dirichlet spaces with superharmonic weights induced by positive Borel measures $\unicode[STIX]{x1D707}$ on the open unit disk. Denote by $M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ Möbius invariant function spaces generated by ${\mathcal{D}}_{\unicode[STIX]{x1D707}}$. In this paper, we investigate the relation among ${\mathcal{D}}_{\unicode[STIX]{x1D707}}$, $M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ and some Möbius invariant function spaces, such as the space $BMOA$ of analytic functions on the open unit disk with boundary values of bounded mean oscillation and the Dirichlet space. Applying the relation between $BMOA$ and $M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$, under the assumption that the weight function $K$ is concave, we characterize the function $K$ such that ${\mathcal{Q}}_{K}=BMOA$. We also describe inner functions in $M({\mathcal{D}}_{\unicode[STIX]{x1D707}})$ spaces.

At the ANZIAM conference in Hobart in February 2018, there were several talks on the solution of Laplace problems in multiply connected domains by means of conformal mapping. It appears to be not widely known that such problems can also be solved by the elementary method of series expansions with coefficients determined by least-squares fitting on the boundary. (These are not convergent series; the coefficients depend on the degree of the approximation.) Here we give a tutorial introduction to this method, which converges at an exponential rate if the boundary data are sufficiently well-behaved. The mathematical foundations go back to Runge in 1885 and Walsh in 1929. One of our examples involves an approximate Cantor set with up to 2048 components.

While the existence of conformal mappings between doubly connected domains is characterized by their conformal moduli, no such characterization is available for harmonic diffeomorphisms. Intuitively, one expects their existence if the domain is not too thick compared to the codomain. We make this intuition precise by showing that for a Dini-smooth doubly connected domain Ω* there exists a ε > 0 such that for every doubly connected domain Ω with ModΩ* < ModΩ < ModΩ* + ε there exists a harmonic diffeomorphism from Ω onto Ω*.

In this paper, a new formulation is proposed to evaluate the origin intensity factors (OIFs) in the singular boundary method (SBM) for solving 3D potential problems with Dirichlet boundary condition. The SBM is a strong-form boundary discretization collocation technique and is mathematically simple, easy-to-program, and free of mesh. The crucial step in the implementation of the SBM is to determine the OIFs which isolate the singularities of the fundamental solutions. Traditionally, the inverse interpolation technique (IIT) is adopted to calculate the OIFs on Dirichlet boundary, which is time consuming for large-scale simulation. In recent years, the new methodology has been developed to efficiently calculate the OIFs on Neumann boundary, but the Dirichlet problem remains an open issue. This study employs the subtracting and adding-back technique based on the integration of the fundamental solution over the whole boundary to develop a new formulation of the OIFs on 3D Dirichlet boundary. Several problems with varied domain shapes and boundary conditions are carried out to validate the effectiveness and feasibility of the proposed scheme in comparison with the SBM based on inverse interpolation technique, the method of fundamental solutions, and the boundary element method.

The main aim of this article is to establish analogues of Landau’s theorem for solutions to the 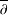$\overline{\unicode[STIX]{x2202}}$-equation in Dirichlet-type spaces.

The family ${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ of orientation-preserving harmonic functions $f=h+\overline{g}$ in the unit disc $\mathbb{D}$ (normalised in the standard way) satisfying

$$\begin{eqnarray}h^{\prime }(z)+g^{\prime }(z)=\frac{1}{(1+\unicode[STIX]{x1D706}z)(1+\overline{\unicode[STIX]{x1D706}}z)},\quad z\in \mathbb{D},\end{eqnarray}$$

$\unicode[STIX]{x1D706}\in \unicode[STIX]{x2202}\mathbb{D}$

${\mathcal{F}}_{\unicode[STIX]{x1D706}}$

We study properties of the simply connected sets in the complex plane, which are finite unions of domains convex in the horizontal direction. These considerations allow us to state new univalence criteria for complex-valued local homeomorphisms. In particular, we apply our results to planar harmonic mappings obtaining generalisations of the shear construction theorem due to Clunie and Sheil-Small [‘Harmonic univalent functions’, Ann. Acad. Sci. Fenn. Ser. A. I. Math.9 (1984), 3–25].

In this paper, we present accurate and economic integration quadratures for hypersingular functions over three simple geometric shapes in ℝ 3 (spheres, cubes, and cylinders). The quadrature nodes are made of the tensor-product of 1-D Gauss nodes on [–1,1] for non-periodic variables or uniform nodes on [0,2π] or [0,π] for periodic ones. The quadrature weights are converted from a brute-force integration of the hypersingular function through interpolating the smooth component of the integrand. Numerical results are presented to validate the accuracy and efficiency of computing hypersingular integrals, as in the computations of Cauchy principal values, with a minimum number of quadrature nodes. The pre-calculated quadrature tables can be then readily used to implement Nyström collocation methods of hypersingular volume integral equations such as the one for Maxwell equations.

We present DASHMM, a general library implementing multipole methods (including both Barnes-Hut and the Fast Multipole Method). DASHMM relies on dynamic adaptive runtime techniques provided by the HPX-5 system to parallelize the resulting multipole moment computation. The result is a library that is easy-to-use, extensible, scalable, efficient, and portable. We present both the abstractions defined by DASHMM as well as the specific features of HPX-5 that allow the library to execute scalably and efficiently.

In this paper, we study quasiconformal extensions of harmonic mappings. Utilizing a complex parameter, we build a bridge between the quasiconformal extension theorem for locally analytic functions given by Ahlfors [‘Sufficient conditions for quasiconformal extension’, Ann. of Math. Stud.79 (1974), 23–29] and the one for harmonic mappings recently given by Hernández and Martín [‘Quasiconformal extension of harmonic mappings in the plane’, Ann. Acad. Sci. Fenn. Math.38 (2) (2013), 617–630]. We also give a quasiconformal extension of a harmonic Teichmüller mapping, whose maximal dilatation estimate is asymptotically sharp.

We present a simple, accurate method for computing singular or nearly singular integrals on a smooth, closed surface, such as layer potentials for harmonic functions evaluated at points on or near the surface. The integral is computed with a regularized kernel and corrections are added for regularization and discretization, which are found from analysis near the singular point. The surface integrals are computed from a new quadrature rule using surface points which project onto grid points in coordinate planes. The method does not require coordinate charts on the surface or special treatment of the singularity other than the corrections. The accuracy is about O(h3), where h is the spacing in the background grid, uniformly with respect to the point of evaluation, on or near the surface. Improved accuracy is obtained for points on the surface. The treecode of Duan and Krasny for Ewald summation is used to perform sums. Numerical examples are presented with a variety of surfaces.

We present RECFMM, a program representation and implementation of a recursive scheme for parallelizing the adaptive fast multipole method (FMM) on shared-memory computers. It achieves remarkable high performance while maintaining mathematical clarity and flexibility. The parallelization scheme signifies the recursion feature that is intrinsic to the FMM but was not well exploited. The program modules of RECFMM constitute a map between numerical computation components and advanced architecture mechanisms. The mathematical structure is preserved and exploited, not obscured nor compromised, by parallel rendition of the recursion scheme. Modern software system—CILK in particular, which provides graph-theoretic optimal scheduling in adaptation to the dynamics in parallel execution—is employed. RECFMM supports multiple algorithm variants that mark the major advances with low-frequency interaction kernels, and includes the asymmetrical version where the source particle ensemble is not necessarily the same as the target particle ensemble. We demonstrate parallel performance with Coulomb and screened Coulomb interactions.

In this paper, for the convolution and convex combination of harmonic mappings, the radii of univalence, full convexity and starlikeness of order $\unicode[STIX]{x1D6FC}$ are explored. All results are sharp. By way of application, the univalent radius and the Bloch constant of the convolution of two bounded harmonic mappings are obtained.

In this paper we present the basic tools of a fractional function theory in higher dimensions by means of a fractional correspondence to the Weyl relations via fractional Riemann–Liouville derivatives. A Fischer decomposition, Almansi decomposition, fractional Euler and Gamma operators, monogenic projection, and basic fractional homogeneous powers are constructed. Moreover, we establish the fractional Cauchy–Kovalevskaya extension (FCK extension) theorem for fractional monogenic functions defined on ℝd . Based on this extension principle, fractional Fueter polynomials, forming a basis of the space of fractional spherical monogenics, i.e. fractional homogeneous polynomials, are introduced. We study the connection between the FCK extension of functions of the form xPl and the classical Gegenbauer polynomials. Finally, we present an example of an FCK extension.

In this paper, we study the selectivity of the potassium channel KcsA by a recently developed image-charge solvation method (ICSM) combined with molecular dynamics simulations. The hybrid solvation model in the ICSM is able to demonstrate atomistically the function of the selectivity filter of the KcsA channel when potassium and sodium ions are considered and their distributions inside the filter are simulated. Our study also shows that the reaction field effect, explicitly accounted for through image charge approximation in the ICSM model, is necessary in reproducing the correct selectivity property of the potassium channels.

In this paper, we will present a high-order, well-conditioned boundary element method (BEM) based on Müller's hypersingular second kind integral equation formulation to accurately compute electrostatic potentials in the presence of inhomogeneity embedded within layered media. We consider two types of inhomogeneities: the first one is a simple model of an ion channel which consists of a finite height cylindrical cavity embedded in a layered electrolytes/membrane environment, and the second one is a Janus particle made of two different semi-spherical dielectric materials. Both types of inhomogeneities have relevant applications in biology and colloidal material, respectively. The proposed BEM gives condition numbers, allowing fast convergence of iterative solvers compared to previous work using first kind of integral equations. We also show that the second order basis converges faster and is more accurate than the first order basis for the BEM.

We discuss the existence of finite critical trajectories connecting two zeros in certain families of quadratic differentials. In addition, we reprove some results about the support of the limiting root-counting measures of the generalised Laguerre and Jacobi polynomials with varying parameters.