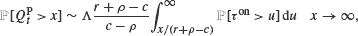Refine listing
Actions for selected content:
1446 results in 60Kxx
Tightness of the stationary waiting time in heavy traffic
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 3 / September 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 788-794
- Print publication:
- September 1999
-
- Article
- Export citation
The distribution of general final state random variables for stochastic epidemic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 473-491
- Print publication:
- June 1999
-
- Article
- Export citation
Central limit theorems for multivariate semi-Markov sequences and processes, with applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 415-432
- Print publication:
- June 1999
-
- Article
- Export citation
A laplace transform representation in a class of renewal queueing and risk processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 570-584
- Print publication:
- June 1999
-
- Article
- Export citation
Setups in polling models: does it make sense to set up if no work is waiting?
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 585-592
- Print publication:
- June 1999
-
- Article
- Export citation
On the convergence to stationarity of the many-server Poisson queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 546-557
- Print publication:
- June 1999
-
- Article
- Export citation
On the time-dependent occupancy and backlog distributions for the GI/G/∞ queue
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 558-569
- Print publication:
- June 1999
-
- Article
- Export citation
Recurrent ring dynamics in two-dimensional excitable cellular automata
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 492-511
- Print publication:
- June 1999
-
- Article
- Export citation
Tail probabilities for non-standard risk and queueing processes with subexponential jumps
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 422-447
- Print publication:
- June 1999
-
- Article
- Export citation
Quermass-interaction processes: conditions for stability
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 315-342
- Print publication:
- June 1999
-
- Article
- Export citation
Asymptotic results for multiplexing subexponential on-off processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 394-421
- Print publication:
- June 1999
-
- Article
- Export citation
Loss networks and Markov random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 2 / June 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 403-414
- Print publication:
- June 1999
-
- Article
- Export citation
Large deviations, moderate deviations, and queues with long-range dependent input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 254-278
- Print publication:
- March 1999
-
- Article
- Export citation
The asymptotic final size distribution of multitype chain-binomial epidemic processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 220-234
- Print publication:
- March 1999
-
- Article
- Export citation
Linear stochastic fluid networks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 244-260
- Print publication:
- March 1999
-
- Article
- Export citation
On the supremum distribution of integrated stationary Gaussian processes with negative linear drift
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 135-157
- Print publication:
- March 1999
-
- Article
- Export citation
Existence and positivity of the limit in processes with a branching structure
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 132-138
- Print publication:
- March 1999
-
- Article
- Export citation
Stationarity of a stochastic population flow model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 291-294
- Print publication:
- March 1999
-
- Article
- Export citation
Central limit theorem for wave-functionals of Gaussian processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 158-177
- Print publication:
- March 1999
-
- Article
- Export citation
Delay in polling systems with large switch-over times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 1 / March 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 232-243
- Print publication:
- March 1999
-
- Article
- Export citation