Two related individuals are identical by descent at a genetic locus if they share the same gene copy at that locus due to inheritance from a recent common ancestor. We consider idealized continuous identity by descent (IBD) data in which IBD status is known continuously along chromosomes. IBD data contains information about the relationship between the two individuals, and about the underlying crossover processes. We present a Monte Carlo method for calculating probabilities for IBD data. The method is not restricted to Haldane's Poisson process model of crossing-over but may be used with other models including the chi-square, Kosambi renewal and Sturt models. Results of a simulation study demonstrate that IBD data can be used to distinguish between alternative models for the crossover process.

A unifying technology is introduced for finding explicit closed form expressions for joint moment generating functions of various random quantities associated with some waiting time problems. Sooner and later waiting times are covered for general discrete- and continuous-time models. The models are either Markov chains or semi-Markov processes with a finite number of states. Waiting times associated with generalized phase-type distributions, that are of interest in survival analysis and other areas, are also covered.

We derive some asymptotic results for the rate of convergence to equilibrium for the number of busy servers in an M/M/N/N queue with input rate λN and service rate 1 for N → ∞ in the ‘subcritical’ case λ ∈]0, 1[. These results improve recent contributions of Fricker, Robert and Tibi.

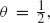We investigate zero-temperature dynamics for a homogeneous ferromagnetic Ising model on the homogeneous tree of degree three (𝕋) with random (i.i.d. Bernoulli) spin configuration at time 0. Letting θ denote the probability that any particular vertex has a +1 initial spin, for infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θ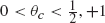c with spin chains almost surely never form for 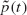θ < θc but almost surely do form in finite time for θ > θc . We relate these results to certain quantities of physical interest, such as the t → ∞ asymptotics of the probability that any particular vertex changes spin after time t.

A (generalized) stochastic fluid system Q is defined as the one-dimensionalSkorokhod reflection of a finite variation process X (with possibly discontinuous paths). We write X as the (not necessarily minimal) difference of two positive measures, A, B, and prove an alternative ‘integral representation’ for Q. This representation forms the basis for deriving a ‘Little's law’ for an appropriately constructed stationary version of Q. For the special case where B is the Lebesgue measure, a distributional version of Little's law is derived. This is done both at the arrival and departure points of the system. The latter result necessitates the consideration of a ‘dual process’ to Q. Examples of models for X, including finite variation Lévy processes with countably many jumps on finite intervals, are given in order to illustrate the ideas and point out potential applications in performance evaluation.

A duality is presented for continuous-time, real-valued, monotone, stochastic recursions driven by processes with stationary increments. A given recursion defines the time evolution of a content process (such as a dam or queue), and it is shown that the existence of the content process implies the existence of a corresponding dual risk process that satisfies a dual recursion. The one-point probabilities for the content process are then shown to be related to the one-point probabilities of the risk process. In particular, it is shown that the steady-state probabilities for the content process are equivalent to the first passage time probabilities for the risk process. A number of applications are presented that flesh out the general theory. Examples include regulated processes with one or two barriers, storage models with general release rate, and jump and diffusion processes.

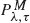In this paper we consider the optimal control of an infinite dam using policies assuming that the input process is a compound Poisson process with a non-negative drift term, and using the total discounted cost and long-run average cost criteria. The results of Lee and Ahn (1998) as well as other well-known results are shown to follow from our results.

Lifetime distributions for multicomponent systems are developed through the interplay of ageing and stress shocks to the system. The ageing process is explicitly modeled by an exponential function with rate affected by the magnitude of stresses from a compound Poisson process shock model. Applications of these life distributions and associated failure rates towards the study of multicomponent system survival are discussed. In particular, we illustrate the behavior of these survival functions in relevant subsets of the parameter space.

The authors prove that certain reliability formulas which link asymptotic availability, mean normal operation time, mean time between failures, mean number of failures over a period of time and asymptotic Vesely rate, and which are well known in the case of modelling using a Markov jump process or an alternating renewal process, are also true in the context of more general modelling.

We consider a network traffic model consisting of an infinite number of sources linked to a server. Sources initiate transmissions to the server at Poisson time points. The duration of each transmission has a heavy-tailed distribution. We show that suitable scalings of the traffic process converge to a totally skewed stable Lévy motion in Skorohod space, equipped with the Skorohod M 1 topology. This allows us to prove a heavy-traffic theorem for a single-server fluid model.

We consider a device that is subject to three types of failures: repairable, non-repairable and failures due to wear-out. This last type is also non-repairable. The times when the system is operative or being repaired follow phase type distributions. When a repairable failure occurs, the operating time of the device decreases, in that the lifetimes between failures are stochastically decreasing according to a geometric process. Following a non-repairable failure or after a previously fixed number of repairs occurs, the device is replaced by a new one. Under these conditions, the functioning of the device can be modelled by a Markov process. We consider two different models depending on whether or not the phase of the operational system at the instants of failure is remembered or not. For both models we derive the stationary distribution of the Markov process, the availability of the device, the rate of occurrence of the different types of failures, and certain quantities of interest.

We study strong asymptotic properties of two types of integral functionals of geometric stochastic processes. These integral functionals are of interest in financial modelling, yielding various option pricings, annuities, etc., by appropriate selection of the processes in their respective integrands. We show that under fairly general conditions on the latter processes the logs of the integral functionals themselves asymptotically behave like appropriate sup functionals of the processes in the exponents of their respective integrands. We illustrate the possible use and applications of these strong invariance theorems by listing and elaborating on several examples.

We define a class of anticipative flows on Poisson space and compute its Radon-Nikodym derivative. This result is applied to statistical testing in an anticipative queueing problem.

We study the following stochastic investment model: opportunities occur randomly over time, following a renewal process with mean interarrival time d, and at each of them the decision-maker can choose a distribution for an instantaneous net gain (or loss) from the set of all probability measures that have some prespecified expected value e and for which his maximum possible loss does not exceed his current capital. Between the investments he spends money at some constant rate. The objective is to avoid bankruptcy as long as possible. For the case e>d we characterize a strategy maximizing the probability that ruin never occurs. It is proved that the optimal value function is a concave function of the initial capital and uniquely determined as the solution of a fixed point equation for some intricate operator. In general, two-point distributions suffice; furthermore, we show that the cautious strategy of always taking the deterministic amount e is optimal if the interarrival times are hyperexponential, and, in the case of bounded interarrival times, is optimal ‘from some point on’, i.e. whenever the current capital exceeds a certain threshold. In the case e = 0 we consider a class of natural objective functions for which the optimal strategies are non-stationary and can be explicitly determined.

We consider a multiserver queue in the heavy-traffic regime introduced and studied by Halfin and Whitt who investigated the case of a single customer class with exponentially distributed service times. Our purpose is to extend their analysis to a system with multiple customer classes, priorities, and phase-type service distributions. We prove a weak convergence limit theorem showing that a properly defined and normalized queue length process converges to a particular K-dimensional diffusion process, where K is the number of phases in the service time distribution. We also show that a properly normalized waiting time process converges to a simple functional of the limit diffusion for the queue length.

In, Tory and Pickard show that a simple subclass of unilateral AR processes identifies with Gaussian Pickard random fields on Z 2. First, we extend this result to the whole class of unilateral AR processes, by showing that they all satisfy a Pickard-type property, under which correlation matching and maximum entropy properties are assessed. Then, it is established that the Pickard property provides the ‘missing’ equations that complement the two-dimensional Yule-Walker equations, in the sense that the conjunction defines a one-to-one mapping between the set of AR parameters and a set of correlations. It also implies Markov chain conditions that allow exact evaluation of the likelihood and an exact sampling scheme on finite lattices.

We establish new multidimensional martingales for Markov additive processes and certain modifications of such processes (e.g., such processes with reflecting barriers). These results generalize corresponding one-dimensional martingale results for Lévy processes. This martingale is then applied to various storage processes, queues and Brownian motion models.

The lifelengths of components of a system are usually dependent due to the common random production and operating environments. In this paper, we introduce a multi-variate pure jump Markov process to describe a large class of damage processes on various system components driven by common environmental shocks, and establish some dependence properties (association) for such a process and its multivariate increment process. These strong association properties describe both spatial dependence and temporal dependence of a multivariate pure jump process, and also provide a vehicle to derive some structural properties of component lifelengths of the systems operating in such an environment. Some bounds for the joint survival functions of component lifelengths are also obtained.

This paper describes the limiting asymptotic behaviour of a long cascade of linear reservoirs fed by stationary inflows into the first reservoir. We show that the storage in the nth reservoir becomes asymptotically deterministic as n → ∞, and establish a central limit theorem for the random fluctuations about the deterministic approximation. In addition, we prove a large deviations theorem that provides precise logarithmic asymptotics for the tail probabilities associated with the storage in the nth reservoir when n is large.

We study a system of interacting renewal processes which is a model for neuronal activity. We show that the system possesses an exponentially large number (with respect to the number of neurons in the network) of limiting configurations of the ‘firing neurons’. These we call patterns. Furthermore, under certain conditions of symmetry we find an algorithm to control limiting patterns by means of the connection parameters.