Refine listing
Actions for selected content:
1446 results in 60Kxx
Disasters in a Markovian inventory system for perishable items
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 61-75
- Print publication:
- March 2001
-
- Article
- Export citation
The busy cycle of the reflected superposition of Brownian motion and a compound Poisson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 255-261
- Print publication:
- March 2001
-
- Article
- Export citation
Analysis of a phase transition phenomenon in packet networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 260-280
- Print publication:
- March 2001
-
- Article
- Export citation
Restarting search algorithms with applications to simulated annealing
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 242-259
- Print publication:
- March 2001
-
- Article
- Export citation
Regenerative processes in the infinite mean cycle case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 165-179
- Print publication:
- March 2001
-
- Article
- Export citation
The structured coalescent process with weak migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-17
- Print publication:
- March 2001
-
- Article
- Export citation
Monotone Markov processes with respect to the reversed hazard rate ordering: an application to reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 195-208
- Print publication:
- March 2001
-
- Article
- Export citation
Analysis of the busy period for the M/M/c queue: an algorithmic approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-222
- Print publication:
- March 2001
-
- Article
- Export citation
Some new results involving the NBU(2) class of life distributions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 242-247
- Print publication:
- March 2001
-
- Article
- Export citation
Some asymptotic results for transient random walks with applications to insurance risk
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 108-121
- Print publication:
- March 2001
-
- Article
- Export citation
The annihilating process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 223-231
- Print publication:
- March 2001
-
- Article
- Export citation
Geometric renewal convergence rates from hazard rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 180-194
- Print publication:
- March 2001
-
- Article
- Export citation
Optimal repair/replacement policy for a general repair model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 206-222
- Print publication:
- March 2001
-
- Article
- Export citation
Inequalities for the GI/M/1/n loss system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 232-234
- Print publication:
- March 2001
-
- Article
- Export citation
Priority queueing model with changeover times and switching threshold
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue A / 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 263-273
- Print publication:
- 2001
-
- Article
- Export citation
Lower bounds for point-to-point wandering exponents in Euclidean first-passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1061-1073
- Print publication:
- December 2000
-
- Article
- Export citation
Sharp results on convergence rates for the distribution of GI/M/1/K queues as K tends to infinity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1010-1019
- Print publication:
- December 2000
-
- Article
- Export citation
Cell loss probability for M/G/1 and time-slotted queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1149-1156
- Print publication:
- December 2000
-
- Article
- Export citation
Loss asymptotics in large buffers fed by heterogeneous long-tailed sources
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1168-1189
- Print publication:
- December 2000
-
- Article
- Export citation
Stochastic domination and Markovian couplings
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1064-1076
- Print publication:
- December 2000
-
- Article
- Export citation
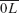 . Here, for Euclidean models in dimension
. Here, for Euclidean models in dimension 