Refine listing
Actions for selected content:
1446 results in 60Kxx
Quasi-renewal estimates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 269-275
- Print publication:
- March 2000
-
- Article
- Export citation
Chaoticity on path space for a queueing network with selection of the shortest queue among several
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 198-211
- Print publication:
- March 2000
-
- Article
- Export citation
Recursive estimation of distributional fix-points
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 73-87
- Print publication:
- March 2000
-
- Article
- Export citation
Moments based approximation for the stationary distribution of a random walk in Z + with an application to the M/GI/1/n queueing system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 290-299
- Print publication:
- March 2000
-
- Article
- Export citation
A general minimal repair model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 187-197
- Print publication:
- March 2000
-
- Article
- Export citation
A fluid queue with a finite buffer and subexponential input
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 221-243
- Print publication:
- March 2000
-
- Article
- Export citation
Asymptotic bounds for the fluid queue fed by sub-exponential On/Off sources
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 244-255
- Print publication:
- March 2000
-
- Article
- Export citation
A perturbation method for the structured coalescent with strong migration
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 148-167
- Print publication:
- March 2000
-
- Article
- Export citation
Jump-type Fleming-Viot processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 140-158
- Print publication:
- March 2000
-
- Article
- Export citation
A note on bias optimality in controlled queueing systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 300-305
- Print publication:
- March 2000
-
- Article
- Export citation
Queueing networks with instantaneous movements: a unified approach by quasi-reversibility
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 284-313
- Print publication:
- March 2000
-
- Article
- Export citation
A join the shorter queue model in heavy traffic
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 212-223
- Print publication:
- March 2000
-
- Article
- Export citation
Estimation of critical values in interacting particle systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 118-125
- Print publication:
- March 2000
-
- Article
- Export citation
Markov random fields and percolation on general graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 39-66
- Print publication:
- March 2000
-
- Article
-
- You have access
- Export citation
NWU property of a class of random sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 283-289
- Print publication:
- March 2000
-
- Article
- Export citation
On the optimality and the asymptotic optimality of the smallest weighted available buffer policy
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 31 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1118-1150
- Print publication:
- December 1999
-
- Article
- Export citation
A note on losses in M/GI/1/n queues
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1240-1243
- Print publication:
- December 1999
-
- Article
- Export citation
Reliability of a system with Poisson inspection times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1140-1154
- Print publication:
- December 1999
-
- Article
- Export citation
On the rates of convergence of Erlang's model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1167-1184
- Print publication:
- December 1999
-
- Article
- Export citation
Bounded normal approximation in simulations of highly reliable Markovian systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 974-986
- Print publication:
- December 1999
-
- Article
- Export citation
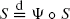 of implicit renewal theory appears where the real random variable
of implicit renewal theory appears where the real random variable 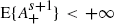 for an
for an 