Refine listing
Actions for selected content:
1446 results in 60Kxx
A stochastic covariate failure model for assessing system reliability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 761-767
- Print publication:
- September 2001
-
- Article
- Export citation
On the total time spent in records by a discrete uniform sequence
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 768-775
- Print publication:
- September 2001
-
- Article
- Export citation
Lundberg inequalities for renewal equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 674-689
- Print publication:
- September 2001
-
- Article
- Export citation
On the existence of the stable birth-type distribution in a general branching process cell cycle model with unequal cell division
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 685-695
- Print publication:
- September 2001
-
- Article
- Export citation
An asymptotic expansion for the expectation of an age-dependent branching process with a submultiplicative estimate of the remainder
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 807-814
- Print publication:
- September 2001
-
- Article
- Export citation
Asymptotic expansions in multidimensional Markov renewal theory and first passage times for Markov random walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 652-673
- Print publication:
- September 2001
-
- Article
- Export citation
On the stability of a batch clearing system with Poisson arrivals and subadditive service times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 621-634
- Print publication:
- September 2001
-
- Article
-
- You have access
- Export citation
Shocks, runs and random sums
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 438-448
- Print publication:
- June 2001
-
- Article
- Export citation
On the convergence and limits of certain matrix sequences arising in quasi-birth-and-death Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 519-541
- Print publication:
- June 2001
-
- Article
- Export citation
Sufficient conditions for long-range count dependence of stationary point processes on the real line
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 570-581
- Print publication:
- June 2001
-
- Article
- Export citation
Finite-size corrections to Poisson approximations of rare events in renewal processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 554-569
- Print publication:
- June 2001
-
- Article
- Export citation
Random bisection and evolutionary walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 582-596
- Print publication:
- June 2001
-
- Article
- Export citation
Average optimal policies in a controlled queueing system with dual admission control
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 369-385
- Print publication:
- June 2001
-
- Article
- Export citation
On a coverage process ranging from the Boolean model to the Poisson–Voronoi tessellation with applications to wireless communications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 293-323
- Print publication:
- June 2001
-
- Article
- Export citation
Signatures of indirect majority systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 597-603
- Print publication:
- June 2001
-
- Article
- Export citation
Burn-in procedures for a generalized model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 542-553
- Print publication:
- June 2001
-
- Article
- Export citation
The M/G/1 queue with two service speeds
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 520-540
- Print publication:
- June 2001
-
- Article
- Export citation
Stochastic multi-type SIR epidemics among a population partitioned into households
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 99-123
- Print publication:
- March 2001
-
- Article
- Export citation
Empirical convergence rates for continuous-time Markov chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 262-269
- Print publication:
- March 2001
-
- Article
- Export citation
Spectrally negative Lévy processes with applications in risk theory
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 1 / March 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 281-291
- Print publication:
- March 2001
-
- Article
- Export citation
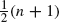 , and use this to show that the expected lifetime of an
, and use this to show that the expected lifetime of an 