Let ℱ be a countable plane triangulation embedded in ℝ2 in such a way that no bounded region contains more than finitely many vertices, and let Pp be Bernoulli (p) product measure on the vertex set of ℱ. Let E be the event that a fixed vertex belongs to an infinite path whose vertices alternate states sequentially. It is shown that the AB percolation probability function θΑΒ (p) = Pp (E) is non-decreasing in p for 0 ≦ p ≦ ½. By symmetry, θ AΒ (p) is therefore unimodal on [0, 1]. This result partially verifies a conjecture due to Halley and stands in contrast to the examples of Łuczak and Wierman.

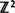We introduce and study a novel type of first-passage percolation problem on where the associated first-passage time measures the density of interface between two types of sites. If the types, designated + and –, are independently assigned their values with probability p and (1 — p) respectively, we show that the density of interface is non-zero provided that both species are subcritical with regard to percolation, i.e. pc > p > 1 – pc. Furthermore, we show that as p ↑ pc or p ↓ (1 – p c), the interface density vanishes with scaling behavior identical to the correlation length of the site percolation problem.

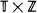For an independent percolation model on , where 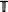is a homogeneous tree and 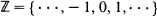is a one-dimensional lattice, it is shown, by verifying that the triangle condition is satisfied, that the percolation probability 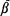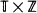θ (p) is a continuous function of p at the critical point pc, and the critical exponents , γ, δ, and Δ exist and take their mean-field values. Some analogous results for Markov fields on are also obtained.

It is known [8] that a certain class of bond-decorated graphs exhibits multiple AB percolation phase transitions. Sufficient conditions are given under which the corresponding AB percolation critical probabilities may be identified as points of intersection of the graph of a certain polynomial with the boundary of the percolative region of an associated two-parameter bond-site percolation model on the underlying undecorated graph. The main result of the article is used to prove that the graphs in [8] exhibit multiple AB percolation critical probabilities. The possibility of identifying AB percolation critical exponents with corresponding limits for the bond-site model is discussed.

We give upper bounds on the critical values for oriented percolation and some interacting particle systems by computing their behavior on small finite sets.