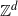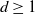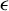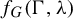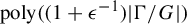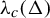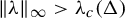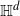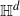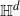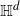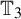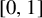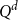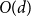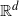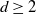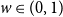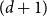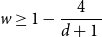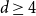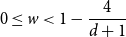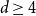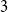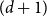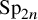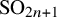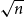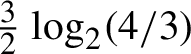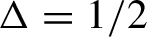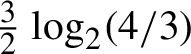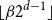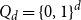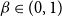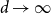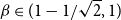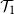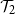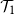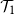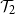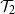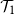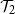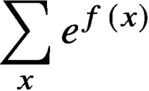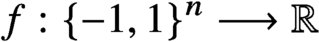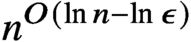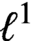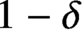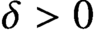Refine listing
Actions for selected content:
165 results in 82Bxx
Differences between Lyapunov exponents for the simple random walk in Bernoulli potentials
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 82-103
- Print publication:
- March 2024
-
- Article
- Export citation
Counting independent sets in amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 24 May 2023, pp. 958-1012
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
Thin-ended clusters in percolation in
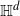 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
A factor of i.i.d. with uniform marginals and infinite clusters spanned by equal labels
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 22 December 2022, pp. 3707-3725
- Print publication:
- November 2023
-
- Article
- Export citation
Supercritical site percolation on the hypercube: small components are small
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 25 November 2022, pp. 422-427
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bose–Einstein condensation for particles with repulsive short-range pair interactions in a Poisson random external potential in
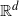 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 28 October 2022, pp. 382-393
- Print publication:
- June 2023
-
- Article
- Export citation
Uniqueness of the Gibbs measure for the 4-state anti-ferromagnetic Potts model on the regular tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 158-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The direct-connectedness function in the random connection model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 August 2022, pp. 179-222
- Print publication:
- March 2023
-
- Article
- Export citation
Quasi-solvable lattice models for
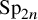 $\operatorname {Sp}_{2n}$ and
$\operatorname {Sp}_{2n}$ and 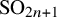 $\operatorname {SO}_{2n+1}$ Demazure atoms and characters
$\operatorname {SO}_{2n+1}$ Demazure atoms and characters
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 18 July 2022, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The diameter of the uniform spanning tree of dense graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 13 May 2022, pp. 1010-1030
-
- Article
- Export citation
A complete proof that square ice entropy is
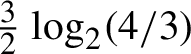 $\tfrac 32\log _{2} (4/3)$
$\tfrac 32\log _{2} (4/3)$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1847-1908
- Print publication:
- June 2023
-
- Article
- Export citation
SINR percolation for Cox point processes with random powers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 March 2022, pp. 227-253
- Print publication:
- March 2022
-
- Article
- Export citation
Independent sets of a given size and structure in the hypercube
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 702-720
-
- Article
- Export citation
A new second-order upper bound for the ground state energy of dilute Bose gases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 18 November 2021, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Expansion for the critical point of site percolation: the first three terms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 28 September 2021, pp. 430-454
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An upper bound for the bond percolation threshold of the cubic lattice by a growth process approach
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 16 September 2021, pp. 677-692
- Print publication:
- September 2021
-
- Article
- Export citation
Continuous phase transitions on Galton–Watson trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 198-228
-
- Article
- Export citation
APPLICATIONS OF SANDPILE ALGORITHMS TO MODELLING EDGE LOCALISED MODE PHENOMENOLOGY IN MAGNETICALLY CONFINED FUSION PLASMAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 351-352
- Print publication:
- October 2021
-
- Article
-
- You have access
- Export citation
More on zeros and approximation of the Ising partition function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 June 2021, e46
-
- Article
-
- You have access
- Open access
- Export citation