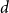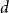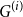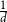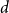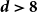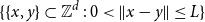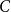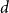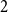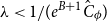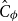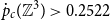Refine listing
Actions for selected content:
165 results in 82Bxx
Inhomogeneous isotropic quantum spin chain associated with the difference Lamé equation
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sampling repulsive Gibbs point processes using random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 63-89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The k-core in percolated dense graph sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 298-318
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-hyperuniformity of Gibbs point processes with short-range interactions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 02 August 2024, pp. 1380-1406
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 05 April 2024, pp. 487-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THERMODYNAMIC FORMALISM FOR AMENABLE GROUPS AND COUNTABLE STATE SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 2647-2711
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Percolation on irregular high-dimensional product graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 20 December 2023, pp. 377-403
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure convergence and second moments of geometric functionals of fractal percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 927-959
- Print publication:
- September 2024
-
- Article
- Export citation
Zeros, chaotic ratios and the computational complexity of approximating the independence polynomial
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 24 November 2023, pp. 459-494
- Print publication:
- March 2024
-
- Article
- Export citation
Spread-out limit of the critical points for lattice trees and lattice animals in dimensions
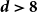 $\boldsymbol{d}\boldsymbol\gt \textbf{8}$
$\boldsymbol{d}\boldsymbol\gt \textbf{8}$
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 20 November 2023, pp. 238-269
-
- Article
- Export citation
Boolean percolation on digraphs and random exchange processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 25 October 2023, pp. 755-766
- Print publication:
- September 2024
-
- Article
- Export citation
Asymptotics of pure dimer coverings on rail yard graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 October 2023, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the zeroes of hypergraph independence polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 65-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height function localisation on trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 50-64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gaussian fluctuations in the equipartition principle for Wigner matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 August 2023, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stable systems with power law conditions for Poisson hail
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 315-353
- Print publication:
- March 2024
-
- Article
- Export citation
Quasipolynomial-time algorithms for Gibbs point processes
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 11 August 2023, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the exponential growth rates of lattice animals and interfaces
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 912-955
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weakly interacting oscillators on dense random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 30 June 2023, pp. 255-278
- Print publication:
- March 2024
-
- Article
- Export citation