Refine listing
Actions for selected content:
165 results in 82Bxx
Asymptotic-Preserving Scheme for the M1-Maxwell System in the Quasi-Neutral Regime
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 301-328
- Print publication:
- February 2016
-
- Article
- Export citation
PINNING ON A DEFECT LINE: CHARACTERIZATION OF MARGINAL DISORDER RELEVANCE AND SHARP ASYMPTOTICS FOR THE CRITICAL POINT SHIFT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 29 January 2016, pp. 305-346
- Print publication:
- April 2018
-
- Article
- Export citation
MODELLING ION, WATER AND ION–WATER CLUSTER ENTERING PEPTIDE NANOTUBES
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 57 / Issue 1 / July 2015
- Published online by Cambridge University Press:
- 02 September 2015, pp. 62-78
-
- Article
-
- You have access
- Export citation
Convergence Study of Moment Approximations for Boundary Value Problems of the Boltzmann-BGK Equation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 14 September 2015, pp. 529-557
- Print publication:
- September 2015
-
- Article
- Export citation
ONE-DIMENSIONAL STOCHASTIC MODELS WITH OPEN BOUNDARIES: INTEGRABILITY, APPLICATIONS AND
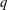 $q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
$q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 520-521
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
TRANSMISSION OF ELASTIC WAVES IN ANISOTROPIC NEMATIC ELASTOMERS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 02 July 2015, pp. 381-396
-
- Article
-
- You have access
- Export citation
AN INTEGRABLE AND EXACTLY SOLVABLE NON-HERMITIAN BCS HAMILTONIAN AND GENERALISED EXCLUSION STATISTICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 346-347
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
First Passage Percolation on Random Geometric Graphs and an Application to Shortest-Path Trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 22 February 2016, pp. 328-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
NEXT ORDER ASYMPTOTICS AND RENORMALIZED ENERGY FOR RIESZ INTERACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 29 May 2015, pp. 501-569
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Continuum AB percolation and AB random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue A / December 2014
- Published online by Cambridge University Press:
- 30 March 2016, pp. 333-344
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Spectral theory for the
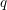 $q$-Boson particle system
$q$-Boson particle system
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 17 September 2014, pp. 1-67
- Print publication:
- January 2015
-
- Article
- Export citation
Growth of a Population of Bacteria in a Dynamical Hostile Environment
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 661-686
- Print publication:
- September 2014
-
- Article
-
- You have access
- Export citation
The Asymptotic Size of the Largest Component in Random Geometric Graphs with Some Applications
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 2 / June 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 307-324
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Percolation of Hard Disks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 235-246
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
Connectivity of Random Geometric Graphs Related to Minimal Spanning Forests
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 04 January 2016, pp. 20-36
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
Maximizing the Size of the Giant
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 4 / December 2012
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1156-1165
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Sharpness in the k-Nearest-Neighbours Random Geometric Graph Model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 617-634
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
Percolation and Connectivity in AB Random Geometric Graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 44 / Issue 1 / March 2012
- Published online by Cambridge University Press:
- 04 January 2016, pp. 21-41
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Percolation of Words on Z d with Long-Range Connections
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 4 / December 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1152-1162
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Russo's Formula, Uniqueness of the Infinite Cluster, and Continuous Differentiability of Free Energy for Continuum Percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 597-610
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation

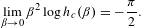

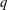
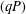

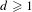
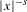
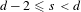
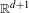
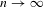
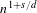
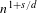
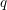
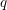
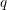
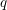
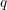
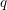
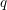
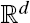 , the
, the 