Refine listing
Actions for selected content:
165 results in 82Bxx
Queues, stores, and tableaux
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1145-1167
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Connectivity of random k-nearest-neighbour graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 1 / March 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-24
- Print publication:
- March 2005
-
- Article
-
- You have access
- Export citation
Coexistence in a two-type continuum growth model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 973-980
- Print publication:
- December 2004
-
- Article
- Export citation
Space filling and depletion
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 41 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 14 July 2016, pp. 691-702
- Print publication:
- September 2004
-
- Article
- Export citation
A random hierarchical lattice: the series-parallel graph and its properties
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 3 / September 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 824-838
- Print publication:
- September 2004
-
- Article
- Export citation
Asymptotic shape in a continuum growth model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 2 / June 2003
- Published online by Cambridge University Press:
- 22 February 2016, pp. 303-318
- Print publication:
- June 2003
-
- Article
- Export citation
Ising models and multiresolution quad-trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 35 / Issue 1 / March 2003
- Published online by Cambridge University Press:
- 01 July 2016, pp. 96-122
- Print publication:
- March 2003
-
- Article
- Export citation
The loss of tension in an infinite membrane with holes distributed according to a Poisson law
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 34 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 01 July 2016, pp. 292-312
- Print publication:
- June 2002
-
- Article
- Export citation
Existence of phase transition of percolation on Sierpiński carpet lattices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 1 / March 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1-10
- Print publication:
- March 2002
-
- Article
- Export citation
Differentiability and monotonicity of expected passage time in Euclidean first-passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 4 / December 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 815-827
- Print publication:
- December 2001
-
- Article
- Export citation
Lower bounds for point-to-point wandering exponents in Euclidean first-passage percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1061-1073
- Print publication:
- December 2000
-
- Article
- Export citation
One-dimensional branching random walks in a Markovian random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1157-1163
- Print publication:
- December 2000
-
- Article
- Export citation
Markov random fields and percolation on general graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 32 / Issue 1 / March 2000
- Published online by Cambridge University Press:
- 01 July 2016, pp. 39-66
- Print publication:
- March 2000
-
- Article
-
- You have access
- Export citation
Phase transition in the random triangle model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 36 / Issue 4 / December 1999
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1101-1115
- Print publication:
- December 1999
-
- Article
- Export citation
First passage percolation and a model for competing spatial growth
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 3 / September 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 683-692
- Print publication:
- September 1998
-
- Article
- Export citation
Stochastic comparison of point random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 868-881
- Print publication:
- December 1997
-
- Article
- Export citation
Asymptotic distributions for the Ehrenfest urn and related random walks
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 33 / Issue 2 / September 1996
- Published online by Cambridge University Press:
- 14 July 2016, pp. 340-356
- Print publication:
- September 1996
-
- Article
- Export citation
Large deviations for discrete and continuous percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 28 / Issue 1 / March 1996
- Published online by Cambridge University Press:
- 01 July 2016, pp. 29-52
- Print publication:
- March 1996
-
- Article
- Export citation
Equality of critical densities in continuum percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 90-104
- Print publication:
- March 1995
-
- Article
- Export citation
Phase transitions of some non-linear stochastic models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 1 / March 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 193-201
- Print publication:
- March 1995
-
- Article
- Export citation
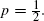
 . Here, for Euclidean models in dimension
. Here, for Euclidean models in dimension 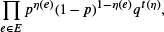
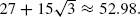 It is furthermore demonstrated that phase transition cannot occur unless
It is furthermore demonstrated that phase transition cannot occur unless 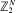 in continuous time
in continuous time 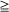 0 can be expressed in terms of binomial distributions; their limit behaviour for
0 can be expressed in terms of binomial distributions; their limit behaviour for 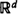 with density ρ, and add the origin as an extra point. Now connect any two points
with density ρ, and add the origin as an extra point. Now connect any two points 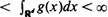 , then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if
, then the two critical densities are non-trivial, i.e. bounded away from 0 and ∞. It is also known that if 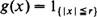 , for some
, for some 