Refine listing
Actions for selected content:
165 results in 82Bxx
The two-type continuum Richardson model: nondependence of the survival of both types on the initial configuration
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 43 / Issue 3 / September 2011
- Published online by Cambridge University Press:
- 01 July 2016, pp. 597-615
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Large Deviations for the Graph Distance in Supercritical Continuum Percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 48 / Issue 1 / March 2011
- Published online by Cambridge University Press:
- 14 July 2016, pp. 154-172
- Print publication:
- March 2011
-
- Article
-
- You have access
- Export citation
PROOF OF THE DETERMINANTAL FORM OF THE SPONTANEOUS MAGNETIZATION OF THE SUPERINTEGRABLE CHIRAL POTTS MODEL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 3 / January 2010
- Published online by Cambridge University Press:
- 25 November 2010, pp. 309-316
-
- Article
-
- You have access
- Export citation
Gibbs Random Fields with Unbounded Spins on Unbounded Degree Graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 856-875
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Branching Process Approach for 2-Sat Thresholds
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 796-810
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
Low degree connectivity of ad-hoc networks via percolation
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 559-576
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
Long-Time Behaviour in a Model of Microtubule Growth
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 268-291
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Sentry Selection in Wireless Networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 42 / Issue 1 / March 2010
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-25
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
Conditional percolation on one-dimensional lattices
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1102-1122
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Does Waste Recycling Really Improve the Multi-Proposal Metropolis–Hastings algorithm? an Analysis Based on Control Variates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 4 / December 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 938-959
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
The existence of quermass-interaction processes for nonlocally stable interaction and nonbounded convex grains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 3 / September 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 664-681
- Print publication:
- September 2009
-
- Article
-
- You have access
- Export citation
Random transceiver networks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 323-343
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Fixed Precision MCMC Estimation by Median of Products of Averages
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 309-329
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
A critical constant for the k nearest-neighbour model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 41 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1-12
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Lakshmibai–Seshadri paths of level-zero shape and one-dimensional sums associated to level-zero fundamental representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1525-1556
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
On the Truncated Long-Range Percolation on Z 2
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 1 / March 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 287-291
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Multitype shape theorems for first passage percolation models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 53-76
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
Maximal avalanches in the Bak-Sneppen model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 3 / September 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 840-851
- Print publication:
- September 2006
-
- Article
-
- You have access
- Export citation
Percolation in the signal to interference ratio graph
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 2 / June 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 552-562
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Random dynamics and thermodynamic limits for polygonal Markov fields in the plane
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 884-907
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
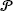 be a Poisson process of intensity one in the infinite plane ℝ
be a Poisson process of intensity one in the infinite plane ℝ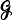 be the random directed graph with vertex set
be the random directed graph with vertex set 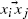 whenever
whenever 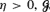 will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from
will almost surely have an infinite directed path, provided the expected number of transceivers that can receive a signal directly from 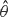 , i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for
, i.e. an estimator which is a ‘median of products of averages’ (MPA). Sufficient conditions are given for 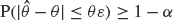 . Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.
. Our main tool is a new bound on the mean-square error, valid also for nonreversible Markov chains on a finite state space.