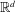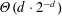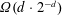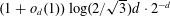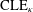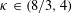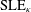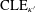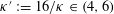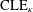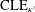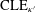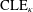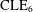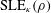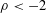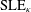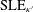Refine listing
Actions for selected content:
165 results in 82Bxx
ON THE HARD SPHERE MODEL AND SPHERE PACKINGS IN HIGH DIMENSIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 14 January 2019, e1
-
- Article
-
- You have access
- Open access
- Export citation
On the critical threshold for continuum AB percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1228-1237
- Print publication:
- December 2018
-
- Article
- Export citation
A multilevel approach towards unbiased sampling of random elliptic partial differential equations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 4 / December 2018
- Published online by Cambridge University Press:
- 29 November 2018, pp. 1007-1031
- Print publication:
- December 2018
-
- Article
- Export citation
Parking on a Random Tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 28 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 23 October 2018, pp. 23-45
-
- Article
- Export citation
Percolation results for the continuum random cluster model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 231-244
- Print publication:
- March 2018
-
- Article
- Export citation
On the phase transition curve in a directed exponential random graph model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 272-301
- Print publication:
- March 2018
-
- Article
- Export citation
CLE PERCOLATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 03 October 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
The Growth Constant of Odd Cutsets in High Dimensions
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 27 / Issue 2 / March 2018
- Published online by Cambridge University Press:
- 14 August 2017, pp. 208-227
-
- Article
- Export citation
On the asymptotics of constrained exponential random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 04 April 2017, pp. 165-180
- Print publication:
- March 2017
-
- Article
- Export citation
On the treewidth of random geometric graphs and percolated grids
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 49-60
- Print publication:
- March 2017
-
- Article
- Export citation
Shearer's point process, the hard-sphere model, and a continuum Lovász local lemma
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 17 March 2017, pp. 1-23
- Print publication:
- March 2017
-
- Article
- Export citation
Computing Optimal Interfacial Structure of Modulated Phases
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 1-15
- Print publication:
- January 2017
-
- Article
- Export citation
A Probabilistic Automatic Steady State Detection Method for the Direct Simulation Monte Carlo
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 5 / November 2016
- Published online by Cambridge University Press:
- 02 November 2016, pp. 1183-1209
- Print publication:
- November 2016
-
- Article
- Export citation
ADDITIVITY PROPERTIES OF SOFIC ENTROPY AND MEASURES ON MODEL SPACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 31 August 2016, e25
-
- Article
-
- You have access
- Open access
- Export citation
On the Widom–Rowlinson Occupancy Fraction in Regular Graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 2 / March 2017
- Published online by Cambridge University Press:
- 09 August 2016, pp. 183-194
-
- Article
- Export citation
Pfaffian Formulas for Spanning Tree Probabilities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 30 May 2016, pp. 118-137
-
- Article
- Export citation
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
SIR epidemics on a scale-free spatial nested modular network
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 137-162
- Print publication:
- March 2016
-
- Article
- Export citation
A comparison of random walks in dependent random environments
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 48 / Issue 1 / March 2016
- Published online by Cambridge University Press:
- 24 March 2016, pp. 199-214
- Print publication:
- March 2016
-
- Article
- Export citation
Inapproximability of the Partition Function for the Antiferromagnetic Ising and Hard-Core Models
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 4 / July 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 500-559
-
- Article
- Export citation