For a homogeneous random walk in the quarter plane with nearest-neighbor transitions, starting from some state (i 0,j 0), we study the event that the walk reaches the vertical axis, before reaching the horizontal axis. We derive a certain integral representation for the probability of this event, and an asymptotic expression for the case when i 0 becomes large, a situation in which the event becomes highly unlikely. The integral representation follows from the solution of a boundary value problem and involves a conformal gluing function. The asymptotic expression follows from the asymptotic evaluation of this integral. Our results find applications in a model for nucleosome shifting, the voter model, and the asymmetric exclusion process.

We prove that a stochastic process of pure coagulation has at any time t ≥ 0 a time-dependent Gibbs distribution if and only if the rates ψ(i, j) of single coagulations are of the form ψ(i; j) = if(j) + jf(i), where f is an arbitrary nonnegative function on the set of positive integers. We also obtain a recurrence relation for weights of these Gibbs distributions that allow us to derive the general form of the solution and the explicit solutions in three particular cases of the function f. For the three corresponding models, we study the probability of coagulation into one giant cluster by time t > 0.

Juggler's exclusion process describes a system of particles on the positive integers where particles drift down to zero at unit speed. After a particle hits zero, it jumps into a randomly chosen unoccupied site. We model the system as a set-valued Markov process and show that the process is ergodic if the family of jump height distributions is uniformly integrable. In a special case where the particles jump according to a set-avoiding memoryless distribution, the process reaches its equilibrium in finite nonrandom time, and the equilibrium distribution can be represented as a Gibbs measure conforming to a linear gravitational potential.

We are concerned with the variation of the supercritical nearest-neighbours contact process such that first infection occurs at a lower rate; it is known that the process survives with positive probability. Regarding the rightmost infected of the process started from one site infected and conditioned to survive, we specify a sequence of space-time points at which its behaviour regenerates and, thus, obtain the corresponding strong law and central limit theorem. We also extend complete convergence in this case.

This paper deals with the problem of discrete and distributed time-delay exponential stability for deterministic and uncertain stochastic high-order neural networks. The concept of a parameter weak coupling linear matrix inequality set (PWCLMIS) is developed. New results are derived in terms of PWCLMIS. Large mixed time delays can be obtained by using this approach. Furthermore, these results are more general than some previous existence results. Two numerical examples are given to show the merit of the approach.

In this paper we show that the continuum-time version of the minority game satisfies the criteria for the application of a theorem on the existence of an invariant measure. We consider the special case of a game with a ‘sufficiently’ asymmetric initial condition, where the number of possible choices for each individual is S = 2 and Γ < +∞. An upper bound for the asymptotic behavior, as the number of agents grows to infinity, of the waiting time for reaching the stationary state is then obtained.

Gabetta and Regazzini (2006b) have shown that finiteness of the initial energy (second moment) is necessary and sufficient for the solution of the Kac's model Boltzmann equation to converge weakly (C b -convergence) to a probability measure on R. Here, we complement this result by providing a detailed analysis of what does actually happen when the initial energy is infinite. In particular, we prove that such a solution converges vaguely (C 0-convergence) to the zero measure (which is identically 0 on the Borel sets of R). More precisely, we prove that the total mass of the limiting distribution splits into two equal masses (of value ½ each), and we provide quantitative estimates on the rate at which such a phenomenon takes place. The methods employed in the proofs also apply in the context of sums of weighted independent and identically distributed random variables x̃ 1, x̃ 2, …, where these random variables have an infinite second moment and zero mean. Then, with T n := ∑j=1 η n λj,n x̃ j , with max1 ≤ j ≤ η n λj,n → 0 (as n → +∞), and ∑j=1 η n λj,n 2 = 1, n = 1, 2, …, the classical central limit theorem suggests that T should in some sense converge to a ‘normal random variable of infinite variance’. Again, in this setting we prove quantitative estimates on the rate at which the mass splits into adherent masses to -∞ and +∞, or to ∞, that are analogous to those we have obtained for the Kac equation. Although the setting in this case is quite classical, we have not uncovered any previous results of a similar type.

With the rapid adoption of transgenic crops, gene flow from transgenic crops to wild relatives through pollen dispersal is of significant concern and warrants both empirical and theoretical studies to assess the risk of introduction of transgenes into wild populations. We propose to use the (biased) voter model in a heterogeneous environment to investigate the effects of recurrent gene flow from transgenic crop to wild relatives. The model is defined on the d-dimensional integer lattice that is divided into two parts, Δ and Z d \ Δ. Individuals carrying the transgene and individuals carrying the wild type gene compete according to the evolution rules of a (biased) voter model on Z d \ Δ, while the process is conditioned to have only individuals carrying the transgene on Δ. Our main findings suggest that unless transgenes confer increased fitness in wild relatives, introgression of transgenes into populations of wild plants is slow and may even be reversible without intervention. Our study also addresses the effects of different spatial planting patterns of transgenic crops on the rate of introgression.

In this paper we introduce the concepts of instantaneous reversibility and instantaneous entropy production rate for inhomogeneous Markov chains with denumerable state spaces. The following statements are proved to be equivalent: the inhomogeneous Markov chain is instantaneously reversible; it is in detailed balance; its entropy production rate vanishes. In particular, for a time-periodic birth-death chain, which can be regarded as a simple version of a physical model (Brownian motors), we prove that its rotation number is 0 when it is instantaneously reversible or periodically reversible. Hence, in our model of Markov chains, the directed transport phenomenon of Brownian motors can occur only in nonequilibrium and irreversible systems.

We study the durations of the avalanches in the maximal avalanche decomposition of the Bak-Sneppen evolution model. We show that all the avalanches in this maximal decomposition have infinite expectation, but only ‘barely’, in the sense that if we made the appropriate threshold a tiny amount smaller (in a certain sense), then the avalanches would have finite expectation. The first of these results is somewhat surprising, since simulations suggest finite expectations.

What is the effect of punching holes at random in an infinite tensed membrane? When will the membrane still support tension? This problem was introduced by Connelly in connection with applications of rigidity theory to natural sciences. The answer clearly depends on the shapes and the distribution of the holes. We briefly outline a mathematical theory of tension based on graph rigidity theory and introduce a probabilistic model for this problem. We show that if the centers of the holes are distributed in ℝ2 according to a Poisson law with density λ > 0, and the shapes are i.i.d. and independent of the locations of their centers, the tension is lost on all of ℝ2 for any λ. After introducing a certain step-by-step dynamic for the loss of tension, we establish the existence of a nonrandom N = N(λ) such that N steps are almost surely enough for the loss of tension. Also, we prove that N(λ) > 2 almost surely for sufficiently small λ. The processes described in the paper are related to bootstrap and rigidity percolation.

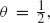We investigate zero-temperature dynamics for a homogeneous ferromagnetic Ising model on the homogeneous tree of degree three (𝕋) with random (i.i.d. Bernoulli) spin configuration at time 0. Letting θ denote the probability that any particular vertex has a +1 initial spin, for infinite spin clusters do not exist at time 0 but we show that infinite ‘spin chains’ (doubly infinite paths of vertices with a common spin) exist in abundance at any time ϵ > 0. We study the structure of the subgraph of 𝕋 generated by the vertices in time-ϵ spin chains. We show the existence of a phase transition in the sense that, for some critical θ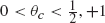c with spin chains almost surely never form for 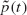θ < θc but almost surely do form in finite time for θ > θc . We relate these results to certain quantities of physical interest, such as the t → ∞ asymptotics of the probability that any particular vertex changes spin after time t.

We prove a sharp upper bound on the number of patterns that can be stored in the Hopfield model if the stored patterns are required to be fixed points of the gradient dynamics. We also show corresponding bounds on the one-step convergence of the sequential gradient dynamics. The bounds coincide with the known lower bounds and confirm the heuristic expectations. The proof is based on a crucial idea of Loukianova (1997) using the negative association properties of some random variables arising in the analysis.

In this paper a simple approximation scheme is proposed for the problem of generating and computing expectations of functionals of a wide class of random variables with values in a compact Lie group. The algorithm is suggested by the time-discretization of an ergodic diffusion leaving invariant the distribution of interest. It is shown to converge as the discretization step goes to zero with the iterations in a natural way.

A problem of regrinding and recycling worn train wheels leads to a Markov population process with distinctive properties, including a product-form equilibrium distribution. A convenient framework for analyzing this process is via the notion of dynamic reversal, a natural extension of ordinary (time) reversal. The dynamically reversed process is of the same type as the original process, which allows a simple derivation of some important properties. The process seems not to belong to any class of Markov processes for which stationary distributions are known.

The distribution (1) used previously by the author to represent polymerisation of several types of unit also prescribes quite general statistics for a random field on a random graph. One has the integral expression (3) for its partition function, but the multiple complex form of the integral makes the nature of the expected saddlepoint evaluation in the thermodynamic limit unclear. It is shown in Section 4 that such an evaluation at a real positive saddlepoint holds, and subsidiary conditions narrowing down the choice of saddlepoint are deduced in Section 6. The analysis simplifies greatly in what is termed the semi-coupled case; see Sections 3, 5 and 7. In Section 8 the analysis is applied to an Ising model on a random graph of fixed degree r + 1. The Curie point of this model is found to agree with that deduced by Spitzer for an Ising model on an r-branching tree. This agreement strengthens the conclusion of ‘locally tree-like' behaviour of the graph, seen as an important property in a number of contexts.