Refine listing
Actions for selected content:
78 results in 82Cxx
Speeding up non-Markovian first-passage percolation with a few extra edges
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 858-886
- Print publication:
- September 2018
-
- Article
- Export citation
Large deviations for randomly connected neural networks: I. Spatially extended systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 944-982
- Print publication:
- September 2018
-
- Article
- Export citation
STOCHASTIC MODELS FOR OPTICALLY TRAPPED NANOWIRES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 343-344
- Print publication:
- October 2018
-
- Article
-
- You have access
- Export citation
Degree-dependent threshold-based random sequential adsorption on random trees
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 50 / Issue 1 / March 2018
- Published online by Cambridge University Press:
- 20 March 2018, pp. 302-326
- Print publication:
- March 2018
-
- Article
- Export citation
Overly determined agents prevent consensus in a generalized Deffuant model on ℤ with dispersed opinions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 722-744
- Print publication:
- September 2017
-
- Article
- Export citation
Comprehensive Studies on Rarefied Jet and Jet Impingement Flows with Gaskinetic Methods
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 06 July 2017, pp. 712-741
- Print publication:
- September 2017
-
- Article
- Export citation
A Flux-Corrected Phase-Field Method for Surface Diffusion
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 22 / Issue 2 / August 2017
- Published online by Cambridge University Press:
- 21 June 2017, pp. 422-440
- Print publication:
- August 2017
-
- Article
- Export citation
A spatial model for selection and cooperation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 522-539
- Print publication:
- June 2017
-
- Article
- Export citation
Analysis of the Closure Approximation for a Class of Stochastic Differential Equations
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 299-330
- Print publication:
- May 2017
-
- Article
- Export citation
Linear Stability of Hyperbolic Moment Models for Boltzmann Equation
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 May 2017, pp. 255-277
- Print publication:
- May 2017
-
- Article
- Export citation
Recovering the Damping Rates of Cyclotron Damped Plasma Waves from Simulation Data
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 947-980
- Print publication:
- April 2017
-
- Article
- Export citation
The entirely coupled region of supercritical contact processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 925-929
- Print publication:
- September 2016
-
- Article
- Export citation
Finite Volume Lattice Boltzmann Method for Nearly Incompressible Flows on Arbitrary Unstructured Meshes
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 20 / Issue 2 / August 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 301-324
- Print publication:
- August 2016
-
- Article
- Export citation
A Semi-Lagrangian Approach for Dilute Non-Collisional Fluid-Particle Flows
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 801-840
- Print publication:
- March 2016
-
- Article
- Export citation
Asymptotic-Preserving Scheme for the M1-Maxwell System in the Quasi-Neutral Regime
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 01 February 2016, pp. 301-328
- Print publication:
- February 2016
-
- Article
- Export citation
Relaxation Schemes for the M1 Model with Space-Dependent Flux: Application to Radiotherapy Dose Calculation
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 15 January 2016, pp. 168-191
- Print publication:
- January 2016
-
- Article
- Export citation
ONE-DIMENSIONAL STOCHASTIC MODELS WITH OPEN BOUNDARIES: INTEGRABILITY, APPLICATIONS AND
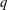 $q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
$q$-DEFORMED KNIZHNIK–ZAMOLODCHIKOV EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 520-521
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Persistence Probability for a Class of Gaussian Processes Related to Random Interface Models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 146-163
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Convergence in a Multidimensional Randomized Keynesian Beauty Contest
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 57-82
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Probability Distribution Function for the Euclidean Distance Between Two Telegraph Processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1172-1193
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation