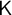Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
6 - Fractional Laplacian in Bounded Domains
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 485-579
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp i-vi
-
- Chapter
- Export citation
7 - Time-Integration of Fractional Models
-
- Book:
- Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024, pp 580-652
-
- Chapter
- Export citation

Spectral and Spectral Element Methods for Fractional Ordinary and Partial Differential Equations
-
- Published online:
- 31 October 2024
- Print publication:
- 14 November 2024
REFERENCE DIGRAPHS OF NON-SELF-REFERENTIAL PARADOXES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 349-366
- Print publication:
- March 2025
-
- Article
- Export citation
The geometry of monotone operator splitting methods
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 487-632
-
- Article
- Export citation
Numerical analysis of physics-informed neural networks and related models in physics-informed machine learning
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 633-713
-
- Article
-
- You have access
- Open access
- Export citation
The Moment-SOS hierarchy: Applications and related topics
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 841-908
-
- Article
- Export citation
ANU volume 33 Cover and Back matter
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, p. b1
-
- Article
-
- You have access
- Export citation
ANU volume 33 Cover and Front matter
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Adaptive finite element methods
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 163-485
-
- Article
-
- You have access
- Open access
- Export citation
Optimal experimental design: Formulations and computations
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 715-840
-
- Article
-
- You have access
- Open access
- Export citation
Splitting methods for differential equations
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 1-161
-
- Article
-
- You have access
- Open access
- Export citation
NORMALISATION FOR NEGATIVE FREE LOGICS WITHOUT AND WITH DEFINITE DESCRIPTIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 18 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 September 2024, pp. 240-272
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ANSELM’S ONTOLOGICAL ARGUMENT AND GRADES OF BEING
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 635-653
- Print publication:
- September 2024
-
- Article
- Export citation
RSL volume 17 issue 3 Cover and Back matter
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 November 2024, pp. b1-b2
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
RSL volume 17 issue 3 Cover and Front matter
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 05 November 2024, pp. f1-f4
- Print publication:
- September 2024
-
- Article
-
- You have access
- Export citation
FINITARY UPPER LOGICISM
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 1172-1247
- Print publication:
- December 2024
-
- Article
- Export citation
RSL volume 17 issue 2 Cover and Front matter
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 27 May 2024, pp. f1-f4
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
RSL volume 17 issue 2 Cover and Back matter
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 27 May 2024, pp. b1-b2
- Print publication:
- June 2024
-
- Article
-
- You have access
- Export citation
 operator for definite descriptions. Rules specific to free logic give rise to new kinds of maximal formulas additional to those familiar from standard intuitionist and classical logic. When
operator for definite descriptions. Rules specific to free logic give rise to new kinds of maximal formulas additional to those familiar from standard intuitionist and classical logic. When  is added it must be ensured that reduction procedures involving replacements of parameters by terms do not introduce new maximal formulas of higher degree than the ones removed. The problem is solved by a rule that permits restricting these terms in the rules for
is added it must be ensured that reduction procedures involving replacements of parameters by terms do not introduce new maximal formulas of higher degree than the ones removed. The problem is solved by a rule that permits restricting these terms in the rules for 

 to parameters or constants. A restricted subformula property for deductions in systems without
to parameters or constants. A restricted subformula property for deductions in systems without  is considered. It is improved upon by an alternative formalisation of free logic building on an idea of Jaśkowski’s. In the classical system the rules for
is considered. It is improved upon by an alternative formalisation of free logic building on an idea of Jaśkowski’s. In the classical system the rules for  require treatment known from normalisation for classical logic with
require treatment known from normalisation for classical logic with