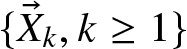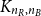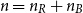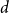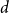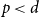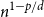Refine search
Actions for selected content:
52629 results in Statistics and Probability
JPR volume 60 issue 4 Cover and Front matter
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 December 2023, pp. f1-f2
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
Daryl John Daley, 4 April 1939 – 16 April 2023 An internationally acclaimed researcher in applied probability and a gentleman of great kindness
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 December 2023, pp. 1516-1531
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Precise large deviations for a multidimensional risk model with regression dependence structure
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 448-457
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal Stopping Methodology for the Secretary Problem with Random Queries – ADDENDUM
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 22 December 2023, p. 1532
- Print publication:
- December 2023
-
- Article
- Export citation
Seasonal mortality amongst UK occupational pension scheme members 2000–2016
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 01 December 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
APR volume 55 issue 4 Cover and Front matter
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 December 2023, pp. f1-f2
- Print publication:
- December 2023
-
- Article
-
- You have access
- Export citation
Chapter Six - Simple Linear Regression
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 204-230
-
- Chapter
- Export citation
Preface
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp xiii-xviii
-
- Chapter
- Export citation
Dedication
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp v-vi
-
- Chapter
- Export citation
Chapter Three - Measures of Location, Spread, and Skewness
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 75-118
-
- Chapter
- Export citation
7 - Introduction to Time Series
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 243-286
-
- Chapter
- Export citation
Appendix D - Solutions
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 745-745
-
- Chapter
- Export citation
2 - Elementary Probability and Statistics
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 35-72
-
- Chapter
- Export citation
Appendix A - Data Set Descriptions
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 707-719
-
- Chapter
- Export citation
Chapter Eighteen - Non-parametric Methods
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 626-659
-
- Chapter
- Export citation
3 - Estimation and Decision-Making
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 73-120
-
- Chapter
- Export citation
Appendices
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp 707-745
-
- Chapter
- Export citation
On minimum spanning trees for random Euclidean bipartite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 30 November 2023, pp. 319-350
-
- Article
- Export citation
8 - Spectral Analysis of Time Series
-
- Book:
- Statistics and Data Visualization in Climate Science with R and Python
- Published online:
- 09 November 2023
- Print publication:
- 30 November 2023, pp 287-328
-
- Chapter
- Export citation
Preface
-
- Book:
- Statistics Using Stata
- Published online:
- 26 January 2024
- Print publication:
- 30 November 2023, pp xv-xviii
-
- Chapter
- Export citation