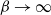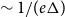Refine search
Actions for selected content:
52379 results in Statistics and Probability
5 - Variance, Higher Moments, and Random Sums
- from Part II - Discrete Random Variables
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 83-115
-
- Chapter
- Export citation
The Excluded Tree Minor Theorem Revisited
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 85-90
-
- Article
- Export citation
Nosocomial outbreak in a respiratory ward caused by the SARS-CoV-2 Omicron BA 5.2.1 subvariant associated with non-severe illness in vaccinated patients
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 26 September 2023, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Factors associated with adverse pregnancy outcomes of maternal syphilis in Henan, China, 2016–2022
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 September 2023, e170
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
R-positivity and the existence of zero-temperature limits of Gibbs measures on nearest-neighbor matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 558-577
- Print publication:
- June 2024
-
- Article
- Export citation
Pertussis outbreak mainly in unvaccinated young children in ultra-orthodox Jewish groups, Jerusalem, Israel 2023
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 22 September 2023, e166
-
- Article
-
- You have access
- Open access
- HTML
- Export citation

Network Analysis
- Integrating Social Network Theory, Method, and Application with R
-
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023
5 - Markov Chains
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 121-143
-
- Chapter
- Export citation
Fertility and ageing – actuarial perspectives
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Measure Theory and Laws of Large Numbers
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 1-39
-
- Chapter
- Export citation
An assessment of model risk in pricing wind derivatives
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 21 September 2023, pp. 479-502
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
6 - Renewal Theory
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 144-162
-
- Chapter
- Export citation
Contents
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp v-vi
-
- Chapter
- Export citation
Index
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 180-182
-
- Chapter
- Export citation
4 - Bounding Probabilities and Expectations
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 95-120
-
- Chapter
- Export citation
2 - Stein’s Method and Central Limit Theorems
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 40-60
-
- Chapter
- Export citation
7 - Brownian Motion
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 163-178
-
- Chapter
- Export citation
References
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp 179-179
-
- Chapter
- Export citation
On the zeroes of hypergraph independence polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 65-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Frontmatter
-
- Book:
- A Second Course in Probability
- Published online:
- 07 September 2023
- Print publication:
- 21 September 2023, pp i-iv
-
- Chapter
- Export citation