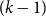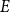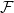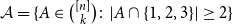Refine search
Actions for selected content:
52379 results in Statistics and Probability
5 - How Are Social Network Data Visualized?
- from Part I - Thinking Structurally
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp 88-114
-
- Chapter
- Export citation
13 - Models for Networks
- from Part III - Making Structural Predictions
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp 301-339
-
- Chapter
- Export citation
Index
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp 447-456
-
- Chapter
- Export citation
Figures
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp ix-xiv
-
- Chapter
- Export citation
1 - Introduction
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp 1-16
-
- Chapter
- Export citation
Part I - Thinking Structurally
-
- Book:
- Network Analysis
- Published online:
- 21 September 2023
- Print publication:
- 05 October 2023, pp 17-114
-
- Chapter
- Export citation
Influenza hospitalisations in Spain between the last influenza and COVID-19 pandemic (2009–2019)
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 04 October 2023, e177
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Association of SARS-CoV-2 viral load with abnormal laboratory characteristics and clinical outcomes in hospitalised COVID-19 patients
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 02 October 2023, e173
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Many Hamiltonian subsets in large graphs with given density
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 110-120
-
- Article
- Export citation
The impact of modeling decisions in statistical profiling
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 02 October 2023, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersecting families without unique shadow
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 91-109
-
- Article
- Export citation
Genetic diversity of Plasmodium vivax in immigrant patients exhibiting severe and non-severe clinical manifestations in northern suburbs of Paris
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 02 October 2023, e127
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal stopping methodology for the secretary problem with random queries
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 578-602
- Print publication:
- June 2024
-
- Article
- Export citation
Structured Replacement Policies for Offshore Wind Turbines
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 355-386
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 465-489
- Print publication:
- June 2024
-
- Article
- Export citation
3 - Common Discrete Random Variables
- from Part II - Discrete Random Variables
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 44-57
-
- Chapter
- Export citation
15 - Estimators for Mean and Variance
- from Part V - Statistical Inference
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 255-264
-
- Chapter
- Export citation
References
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 539-543
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp iv-iv
-
- Chapter
- Export citation
12 - The Poisson Process
- from Part IV - Computer Systems Modeling and Simulation
-
- Book:
- Introduction to Probability for Computing
- Published online:
- 12 September 2023
- Print publication:
- 28 September 2023, pp 210-228
-
- Chapter
- Export citation