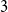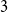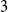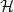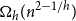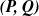Refine search
Actions for selected content:
52379 results in Statistics and Probability
Genetic and epidemiological analyses of infection load and its relationship with psychiatric disorders
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 18 May 2023, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pair degree condition for Hamiltonian cycles in 3-uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 762-781
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intergenerational risk sharing in a defined contribution pension system: analysis with Bayesian optimization
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 515-544
- Print publication:
- September 2023
-
- Article
- Export citation
Neural networks for quantile claim amount estimation: a quantile regression approach
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 17 May 2023, pp. 30-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOVEL APPROACH TO PREDICTIVE ACCURACY TESTING IN NESTED ENVIRONMENTS
-
- Journal:
- Econometric Theory / Volume 41 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 17 May 2023, pp. 35-78
-
- Article
-
- You have access
- Open access
- Export citation
Universal geometric graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 742-761
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An investigation of the seasonal relationships between meteorological factors, water quality, and sporadic cases of Legionnaires’ disease in Washington, DC
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exponential control of the trajectories of iterated function systems with application to semi-strong GARCH
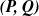 $\boldsymbol{{(P, Q)}}$ models
$\boldsymbol{{(P, Q)}}$ models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1501-1515
- Print publication:
- December 2023
-
- Article
- Export citation
Adverse childhood experiences and craving: Results from an Italian population in outpatient addiction treatment
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 12 May 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INFERENCE ON GARCH-MIDAS MODELS WITHOUT ANY SMALL-ORDER MOMENT
-
- Journal:
- Econometric Theory / Volume 40 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 1422-1455
-
- Article
- Export citation
Index
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 458-464
-
- Chapter
- Export citation
6 - ARIMA(p, d, q)(P, D, Q)F Modeling and Forecasting
- from Part II - Univariate Models of Temporal Dependence
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 245-312
-
- Chapter
- Export citation
Preface
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp xi-xii
-
- Chapter
- Export citation
5 - Stationary Stochastic Processes
- from Part II - Univariate Models of Temporal Dependence
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 189-244
-
- Chapter
- Export citation
References
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 448-457
-
- Chapter
- Export citation
Pyrroloquinoline quinone influences intracellular alpha-synuclein aggregates
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 11 May 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
1 - Introduction to Time Series Data
- from Part I - Descriptive Features of Time Series Data
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 4-57
-
- Chapter
- Export citation
Part I - Descriptive Features of Time Series Data
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 1-3
-
- Chapter
- Export citation
9 - Classical Regression with ARMA Residuals
- from Part III - Multivariate Modeling and Forecasting
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 390-430
-
- Chapter
- Export citation
Part II - Univariate Models of Temporal Dependence
-
- Book:
- Time Series for Data Scientists
- Published online:
- 01 June 2023
- Print publication:
- 11 May 2023, pp 159-161
-
- Chapter
- Export citation