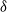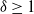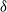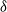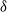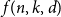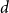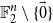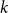Refine search
Actions for selected content:
52379 results in Statistics and Probability
ECT volume 39 issue 3 Cover and Front matter
-
- Journal:
- Econometric Theory / Volume 39 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 24 May 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
HIV sero-status of healthcare workers in Addis Ababa public hospitals post exposure to infected blood and body fluids: A cross-sectional study, October 2022
-
- Journal:
- Epidemiology & Infection / Volume 152 / 2024
- Published online by Cambridge University Press:
- 23 May 2023, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clinical epidemiology and a novel predicting nomogram of central line associated bloodstream infection in burn patients
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 23 May 2023, e90
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Monkeypox: a review of epidemiological modelling studies and how modelling has led to mechanistic insight
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 23 May 2023, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A branching random walk in the presence of a hard wall
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 1-17
- Print publication:
- March 2024
-
- Article
- Export citation
Genomic analysis of an outbreak of toxin gene bearing Corynebacterium diphtheriae in Northern Queensland, Australia reveals high level of genetic similarity
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 22 May 2023, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A first-passage-place problem for integrated diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 55-67
- Print publication:
- March 2024
-
- Article
- Export citation
City data ecosystems between theory and practice: A qualitative exploratory study in seven European cities
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 22 May 2023, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Machine learning approaches for the prediction of serious fluid leakage from hydrocarbon wells
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Averaging for slow–fast piecewise deterministic Markov processes with an attractive boundary
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1439-1468
- Print publication:
- December 2023
-
- Article
- Export citation
Raw driving data of passenger cars considering traffic conditions in Semnan city
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prediction of the COVID-19 transmission: a case study of Pakistan
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Development and external validation of a prognostic tool for nonsevere COVID-19 inpatients
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Kalikow decomposition for counting processes with stochastic intensity and application to simulation algorithms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1469-1500
- Print publication:
- December 2023
-
- Article
- Export citation
Use of portable air purifiers to reduce aerosols in hospital settings and cut down the clinical backlog: a critical analysis
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Distributions of random variables involved in discrete censored δ-shock models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1144-1170
- Print publication:
- December 2023
-
- Article
- Export citation
TESTING FOR ANTICIPATED CHANGES IN SPOT VOLATILITY AT EVENT TIMES
-
- Journal:
- Econometric Theory / Volume 41 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 19 May 2023, pp. 1-34
-
- Article
- Export citation
Association of current hepatitis B virus infection with mortality in adults with sepsis
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 19 May 2023, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint models for cause-of-death mortality in multiple populations
-
- Journal:
- Annals of Actuarial Science / Volume 18 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 18 May 2023, pp. 51-77
-
- Article
- Export citation
Subspace coverings with multiplicities
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 18 May 2023, pp. 782-795
-
- Article
-
- You have access
- Open access
- HTML
- Export citation