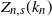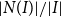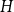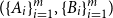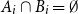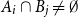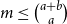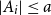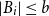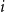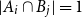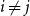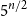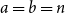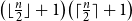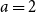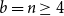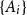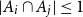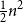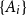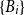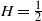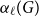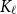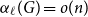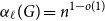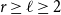Refine search
Actions for selected content:
52379 results in Statistics and Probability
Effectiveness of near-UVA in SARS-CoV-2 inactivation
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 27 April 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Circulation and colonisation of Blastocystis subtypes in schoolchildren of various ethnicities in rural northern Thailand
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 27 April 2023, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mixing time bounds for edge flipping on regular graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 26 April 2023, pp. 1317-1332
- Print publication:
- December 2023
-
- Article
- Export citation
Uniform-in-phase-space data selection with iterative normalizing flows
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approaching the coupon collector’s problem with group drawings via Stein’s method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1352-1366
- Print publication:
- December 2023
-
- Article
-
- You have access
- HTML
- Export citation
Ramsey upper density of infinite graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 5 / September 2023
- Published online by Cambridge University Press:
- 25 April 2023, pp. 703-723
-
- Article
- Export citation
Prevalence of Trypanosoma cruzi infection in a cohort of people living with HIV/AIDS from an urban area
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e72
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERCEPT ESTIMATION IN NONLINEAR SELECTION MODELS
-
- Journal:
- Econometric Theory / Volume 40 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1311-1363
-
- Article
-
- You have access
- Open access
- Export citation
Problems and results on 1-cross-intersecting set pair systems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 691-702
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lower bound for the expected supremum of fractional brownian motion using coupling
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1232-1248
- Print publication:
- December 2023
-
- Article
- Export citation
A physics-based domain adaptation framework for modeling and forecasting building energy systems
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Operationalizing digital self-determination
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NUCLEAR NORM REGULARIZED QUANTILE REGRESSION WITH INTERACTIVE FIXED EFFECTS
-
- Journal:
- Econometric Theory / Volume 40 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1391-1421
-
- Article
- Export citation
Characterization theorems for pseudo cross-variograms
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1219-1231
- Print publication:
- December 2023
-
- Article
- Export citation
Shortcuts for the construction of sub-annual life tables
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 332-350
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
“Insurers” hidden risk from reinsurance recaptures – the perspective of UK annuity writers’
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Clique-factors in graphs with sublinear
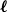 $\boldsymbol\ell$-independence number
$\boldsymbol\ell$-independence number
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 665-681
-
- Article
- Export citation
Expected number of faces in a random embedding of any graph is at most linear
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 682-690
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Open data as an anticorruption tool? Using distributed cognition to understand breakdowns in the creation of transparency data
-
- Journal:
- Data & Policy / Volume 5 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SARS-CoV-2 seroprevalence and determinants for salivary seropositivity among pupils and school staff: a prospective cohort study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation