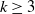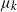Refine search
Actions for selected content:
52379 results in Statistics and Probability
Introduction to the special issue on scientific networks
-
- Journal:
- Network Science / Volume 11 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 1-4
-
- Article
- Export citation
Auto-balanced common shock claim models
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 580-605
-
- Article
- Export citation
Costa’s concavity inequality for dependent variables based on the multivariate Gaussian copula
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 1136-1156
- Print publication:
- December 2023
-
- Article
- Export citation
Breaking of ensemble equivalence for dense random graphs under a single constraint
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1181-1200
- Print publication:
- December 2023
-
- Article
- Export citation
Premium control with reinforcement learning
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 233-257
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling socio-economic mortality at neighbourhood level
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 285-310
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stein’s method and approximating the multidimensional quantum harmonic oscillator
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 855-873
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
ECT volume 39 issue 2 Cover and Front matter
-
- Journal:
- Econometric Theory / Volume 39 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 06 April 2023, pp. f1-f2
-
- Article
-
- You have access
- Export citation
THE ECONOMETRIC THEORY AWARDS 2023
-
- Journal:
- Econometric Theory / Volume 39 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 06 April 2023, p. 442
-
- Article
-
- You have access
- Export citation
ECT volume 39 issue 2 Cover and Back matter
-
- Journal:
- Econometric Theory / Volume 39 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 06 April 2023, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Data and modelling considerations for mental health in life insurance
-
- Journal:
- British Actuarial Journal / Volume 28 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Recruiting controls from an online panel for a case–control study enabled a timely and reliable foodborne Salmonella outbreak investigation, Germany 2021
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 05 April 2023, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
How fast do we forget our past social interactions? Understanding memory retention with parametric decays in relational event models
-
- Journal:
- Network Science / Volume 11 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 267-294
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stochastic comparisons of largest claim and aggregate claim amounts
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 245-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Characterisation of infection-induced SARS-CoV-2 seroprevalence amongst children and adolescents in North Carolina
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 03 April 2023, e63
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Risk-adjusted policies to minimise perioperative staffing shortages during a pandemic: An agent-based simulation study
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 03 April 2023, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hepatitis B in Africa Collaborative Network: cohort profile and analysis of baseline data
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 03 April 2023, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Survival energy models for mortality prediction and future prospects
- Part of
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 377-391
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The relationship between Porphyromonas gingivalis and oesophageal squamous cell carcinoma: a literature review
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 03 April 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A spatial mutation model with increasing mutation rates
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 03 April 2023, pp. 1157-1180
- Print publication:
- December 2023
-
- Article
- Export citation