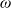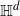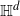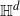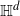Refine search
Actions for selected content:
52379 results in Statistics and Probability
The Bruss–Robertson–Steele inequality
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 1112-1114
- Print publication:
- September 2023
-
- Article
- Export citation
Risk allocation through shapley decompositions, with applications to variable annuities
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 311-331
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Worst-case moments under partial ambiguity
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 443-465
- Print publication:
- May 2023
-
- Article
- Export citation
Target benefit pension plan with longevity risk and intergenerational equity – CORRIGENDUM
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 13 March 2023, p. 488
- Print publication:
- May 2023
-
- Article
-
- You have access
- HTML
- Export citation
A new measure of inaccuracy for record statistics based on extropy
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 207-225
-
- Article
-
- You have access
- HTML
- Export citation
Phase transitions in biased opinion dynamics with 2-choices rule
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 10 March 2023, pp. 227-244
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin-ended clusters in percolation in
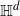 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
8 - Introduction to Relational Databases
- from Part III - Data in Databases
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 103-120
-
- Chapter
-
- You have access
- Open access
- Export citation
Appendix A - Description of HUD data and Analysis
- from 12 - Validation of Models Used by Banks to Estimate Their Allowance for Loan and Lease Losses
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 323-323
-
- Chapter
- Export citation
3 - Data = Content + Structure
- from Part I - Introduction
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 23-36
-
- Chapter
-
- You have access
- Open access
- Export citation
17 - Validation of Risk Management Models in Investment Management
-
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 439-444
-
- Chapter
- Export citation
14 - Best Practices in Data Management
- from Part V - Conclusion
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 209-218
-
- Chapter
-
- You have access
- Open access
- Export citation
Contributors
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp xiii-xiv
-
- Chapter
- Export citation
Part III - Data in Databases
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 101-102
-
- Chapter
-
- You have access
- Open access
- Export citation
8 - COM–Poisson Cure Rate Models
-
- Book:
- The Conway–Maxwell–Poisson Distribution
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 284-311
-
- Chapter
- Export citation
12 - Validation of Models Used by Banks to Estimate Their Allowance for Loan and Lease Losses
-
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 295-330
-
- Chapter
- Export citation
Part IV - Special Types of Data
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 145-146
-
- Chapter
-
- You have access
- Open access
- Export citation
6 - Evaluating Banks’ Value-at-Risk Models during the COVID-19 Crisis
-
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp 104-123
-
- Chapter
- Export citation
10 - Database Fine-Tuning
- from Part III - Data in Databases
-
- Book:
- Data Management for Social Scientists
- Published online:
- 03 March 2023
- Print publication:
- 09 March 2023, pp 135-144
-
- Chapter
-
- You have access
- Open access
- Export citation
Foreword
-
- Book:
- Validation of Risk Management Models for Financial Institutions
- Published online:
- 02 March 2023
- Print publication:
- 09 March 2023, pp xv-xvi
-
- Chapter
- Export citation