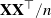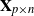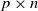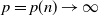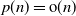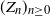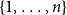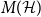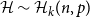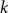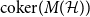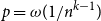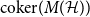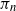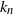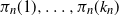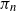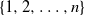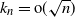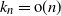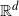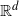Refine search
Actions for selected content:
52379 results in Statistics and Probability
Large deviations of extremal eigenvalues of sample covariance matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1275-1280
- Print publication:
- December 2023
-
- Article
- Export citation
Impact of combination methods on extreme precipitation projections
-
- Journal:
- Annals of Actuarial Science / Volume 17 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 459-478
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting shape for first-passage percolation models on random geometric graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1367-1385
- Print publication:
- December 2023
-
- Article
- Export citation
The use of autoencoders for training neural networks with mixed categorical and numerical features
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 213-232
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bridging the gap between pricing and reserving with an occurrence and development model for non-life insurance claims
-
- Journal:
- ASTIN Bulletin: The Journal of the IAA / Volume 53 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 185-212
- Print publication:
- May 2023
-
- Article
- Export citation
Inequities in COVID-19 Omicron infections and hospitalisations for Māori and Pacific people in Te Manawa Taki Midland region, New Zealand
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 24 April 2023, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-normalized Cramér moderate deviations for a supercritical Galton–Watson process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 1281-1292
- Print publication:
- December 2023
-
- Article
- Export citation
Probabilistic selection and design of concrete using machine learning
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 20 April 2023, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic behaviour of the first positions of uniform parking functions
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 1201-1218
- Print publication:
- December 2023
-
- Article
- Export citation
Modeling complex interactions in a disrupted environment: Relational events in the WTC response
-
- Journal:
- Network Science / Volume 11 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 18 April 2023, pp. 295-323
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Role of latent tuberculosis infection on elevated risk of cardiovascular disease: a population-based cohort study of immigrants in British Columbia, Canada, 1985–2019
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 17 April 2023, e68
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Segregated mobility patterns amplify neighborhood disparities in the spread of COVID-19
-
- Journal:
- Network Science / Volume 11 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 411-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Response to: ‘Use of portable air purifiers to reduce aerosols in hospital settings and cut down the clinical backlog’
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 17 April 2023, e87
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Leveraging Big Data in port state control: An analysis of port state control data and its potential for governance and transparency in the shipping industry
- Part of
-
- Journal:
- Data-Centric Engineering / Volume 4 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A POWERFUL SUBVECTOR ANDERSON–RUBIN TEST IN LINEAR INSTRUMENTAL VARIABLES REGRESSION WITH CONDITIONAL HETEROSKEDASTICITY
-
- Journal:
- Econometric Theory / Volume 40 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 14 April 2023, pp. 957-1002
-
- Article
-
- You have access
- Open access
- Export citation
Uncertain veracity judgments: Does the framing of the question influence deception detection?
-
- Journal:
- Experimental Results / Volume 4 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local limits of spatial inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 14 April 2023, pp. 793-840
- Print publication:
- September 2023
-
- Article
- Export citation
Decreased Neisseria gonorrhoeae genotypic diversity following COVID-19 restrictions in Queensland, Australia 2020
-
- Journal:
- Epidemiology & Infection / Volume 151 / 2023
- Published online by Cambridge University Press:
- 13 April 2023, e67
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-reversible guided Metropolis kernel
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 955-981
- Print publication:
- September 2023
-
- Article
- Export citation