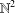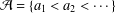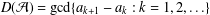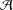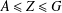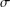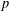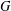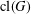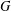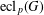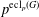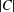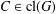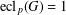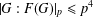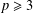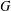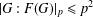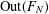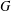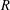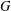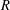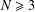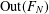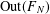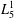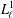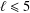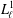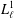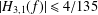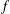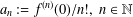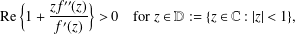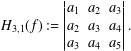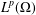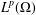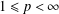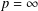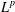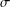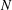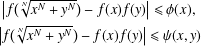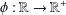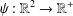Contents
Research Article
VISIBLE POINTS ON EXPONENTIAL CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 353-359
-
- Article
-
- You have access
- Export citation
FINITELY STABLE ADDITIVE BASES
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 360-362
-
- Article
-
- You have access
- Export citation
A NOTE ON THE ERDŐS–GRAHAM THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 363-366
-
- Article
-
- You have access
- Export citation
A VARIATION ON THE THEME OF NICOMACHUS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 367-373
-
- Article
-
- You have access
- Open access
- Export citation
IMPROVING AN INEQUALITY FOR THE DIVISOR FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 374-381
-
- Article
-
- You have access
- Export citation
A NOTE ON THE FUNDAMENTAL THEOREM OF ALGEBRA
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 382-385
-
- Article
-
- You have access
- Export citation
ALEXANDER POLYNOMIALS OF COMPLEX PROJECTIVE PLANE CURVES
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 386-395
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF FINITE PT-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 396-405
-
- Article
-
- You have access
- Export citation
ON
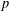 $p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
$p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 406-411
-
- Article
-
- You have access
- Export citation
COUNTING CONJUGACY CLASSES IN
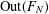 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 412-421
-
- Article
-
- You have access
- Export citation
LEE MONOIDS ARE NONFINITELY BASED WHILE THE SETS OF THEIR ISOTERMS ARE FINITELY BASED
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 422-434
-
- Article
-
- You have access
- Export citation
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
-
- Article
-
- You have access
- Export citation
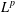 $L^{p}$ -APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
$L^{p}$ -APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 446-452
-
- Article
-
- You have access
- Export citation
INEQUALITIES ASSOCIATED WITH RATIOS OF GAMMA FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 453-458
-
- Article
-
- You have access
- Export citation
ON THE HYPERSTABILITY OF A PEXIDERISED
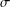 $\unicode[STIX]{x1D70E}$ -QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
$\unicode[STIX]{x1D70E}$ -QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 459-470
-
- Article
-
- You have access
- Export citation
STABILITY OF AN EXPONENTIAL-MONOMIAL FUNCTIONAL EQUATION
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 471-479
-
- Article
-
- You have access
- Export citation
THE HARDY AND HEISENBERG INEQUALITIES IN MORREY SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 480-491
-
- Article
-
- You have access
- Export citation
A REMARK ON THE TRACIAL ROKHLIN PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 492-498
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS ON
 $\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
$\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 499-512
-
- Article
-
- You have access
- Export citation
A SIMPLE PROOF OF THE STRONG LAW OF LARGE NUMBERS WITH RATES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 513-517
-
- Article
-
- You have access
- Export citation