We investigate the representation theory of the crossed-product ${{C}^{*}}$-algebra associated with a compact group $G$ acting on a locally compact space $X$ when the stability subgroups vary discontinuously. Our main result applies when $G$ has a principal stability subgroup or $X$ is locally of finite $G$-orbit type. Then the upper multiplicity of the representation of the crossed product induced from an irreducible representation $V$ of a stability subgroup is obtained by restricting $V$ to a certain closed subgroup of the stability subgroup and taking the maximum of the multiplicities of the irreducible summands occurring in the restriction of $V$. As a corollary we obtain that when the trivial subgroup is a principal stability subgroup; the crossed product is a Fell algebra if and only if every stability subgroup is abelian. A second corollary is that the ${{C}^{*}}$-algebra of the motion group ${{\mathbb{R}}^{n}}\,\rtimes \,\text{SO}\left( n \right)$ is a Fell algebra. This uses the classical branching theorem for the special orthogonal group $\text{SO}\left( n \right)$ with respect to $\text{SO}\left( n-1 \right)$. Since proper transformation groups are locally induced from the actions of compact groups, we describe how some of our results can be extended to transformation groups that are locally proper.

We investigate the numbers of complex zeros of Littlewood polynomials 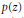$p\left( z \right)$ (polynomials with coefficients {−1, 1}) inside or on the unit circle 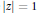$\left| z \right|\,=\,1$, denoted by 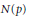$N\left( p \right)$ and 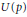$U\left( p \right)$, respectively. Two types of Littlewood polynomials are considered: Littlewood polynomials with one sign change in the sequence of coefficients and Littlewood polynomials with one negative coefficient. We obtain explicit formulas for 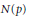$N\left( p \right)$, 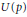$U\left( p \right)$ for polynomials 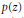$p\left( z \right)$ of these types. We show that if 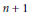$n\,+\,1$ is a prime number, then for each integer 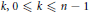$k,\,0\,⩽\,k\,⩽\,n-1$, there exists a Littlewood polynomial 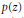$p\left( z \right)$ of degree 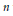$n$ with 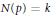$N\left( p \right)\,=\,k$ and 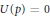$U\left( p \right)\,=\,0$. Furthermore, we describe some cases where the ratios 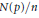$N\left( p \right)/n$ and 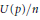$U\left( p \right)/n$ have limits as 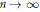$n\,\to \,\infty $ and find the corresponding limit values.

We provide some new local obstructions to approximating tropical curves in smooth tropical surfaces. These obstructions are based on a relation between tropical and complex intersection theories, which is also established here. We give two applications of the methods developed in this paper. First we classify all locally irreducible approximable 3-valent fan tropical curves in a fan tropical plane. Secondly, we prove that a generic non-singular tropical surface in tropical projective 3-space contains finitely many approximable tropical lines if it is of degree 3, and contains no approximable tropical lines if it is of degree 4 or more.

A representation of the central extension of the unitary Lie algebra coordinated with a skew Laurent polynomial ring is constructed using vertex operators over an integral ${{\mathbb{Z}}_{2}}$-lattice. The irreducible decomposition of the representation is explicitly computed and described. As a by-product, some fundamental representations of affine Kac–Moody Lie algebra of type $A_{n}^{\left( 2 \right)}$ are recovered by the new method.

An integer is said to be $y$-friable if its greatest prime factor is less than $y$. In this paper, we obtain estimates for exponential sums over $y$-friable numbers up to $x$ which are non-trivial when $y\,\ge \,\exp \left\{ c \right.\sqrt{\log \,x\,}\log \,\log \,\left. x \right\}$. As a consequence, we obtain an asymptotic formula for the number of $y$-friable solutions to the equation $a\,+\,b\,=\,c$ which is valid unconditionally under the same assumption. We use a contour integration argument based on the saddle point method, as developped in the context of friable numbers by Hildebrand and Tenenbaum, and used by Lagarias, Soundararajan and Harper to study exponential and character sums over friable numbers.

The algebraic cobordism group of a scheme is generated by cycles that are proper morphisms from smooth quasiprojective varieties. We prove that over a field of characteristic zero the quasiprojectivity assumption can be omitted to get the same theory.

Let $p$ be an odd prime. We study the variation of the $p$-rank of the Selmer groups of Abelian varieties with complex multiplication in certain towers of number fields.

In this paper, we give a tropical method for computing Gromov–Witten type invariants of Fano manifolds of special type. This method applies to those Fano manifolds that admit toric degenerations to toric Fano varieties with singularities allowing small resolutions. Examples include (generalized) flag manifolds of type $\text{A}$ and some moduli space of rank two bundles on a genus two curve.

In this paper, we study the explicit geography problem of irregular Gorenstein minimal 3-folds of general type. We generalize the classical Noether–Castelnuovo type inequalities for irregular surfaces to irregular 3-folds according to the Albanese dimension.