Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 18
Idempotents in Noetherian Group Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 366-369
-
- Article
-
- You have access
- Export citation
- Cited by 18
The Approximate Jordan-Hahn Decomposition
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1124-1146
-
- Article
-
- You have access
- Export citation
- Cited by 18
The Poisson Integral of a Singular Measure
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 735-749
-
- Article
-
- You have access
- Export citation
- Cited by 18
On Surface Waves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 271-278
-
- Article
-
- You have access
- Export citation
- Cited by 18
Prolongations and Computational Algebra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 930-949
-
- Article
-
- You have access
- Export citation
- Cited by 18
Semi-Compactness with Respect to a Euclidean Cone
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 29-36
-
- Article
-
- You have access
- Export citation
- Cited by 18
On Higher Moments of Fourier Coefficients of Holomorphic Cusp Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 634-647
-
- Article
-
- You have access
- Export citation
- Cited by 18
Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Erdős Weights
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 710-736
-
- Article
-
- You have access
- Export citation
- Cited by 18
q-Integral and Moment Representations for q-Orthogonal Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 709-735
-
- Article
-
- You have access
- Export citation
- Cited by 18
Maps in Locally Orientable Surfaces and Integrals Over Real Symmetric Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 865-882
-
- Article
-
- You have access
- Export citation
- Cited by 18
SubRiemannian Geometry on the Sphere 𝕊3
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-739
-
- Article
-
- You have access
- Export citation
- Cited by 18
Some Imbedding Theorems for Sobolev Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 517-530
-
- Article
-
- You have access
- Export citation
- Cited by 18
A Theorem on Steiner Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1010-1015
-
- Article
-
- You have access
- Export citation
- Cited by 18
On a Generalization of a Result of Waldspurger
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 105-142
-
- Article
-
- You have access
- Export citation
- Cited by 18
The Expansion Problem with Boundary Conditions at a Finite Set of Points
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 462-479
-
- Article
-
- You have access
- Export citation
- Cited by 18
Polytopes, Valuations, and the Euler Relation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1412-1424
-
- Article
-
- You have access
- Export citation
- Cited by 18
Sur Les Anneaux Reflexifs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1222-1228
-
- Article
-
- You have access
- Export citation
- Cited by 18
Some Results on the Countable Compactness and Pseudocompactness of Hyperspaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1392-1399
-
- Article
-
- You have access
- Export citation
- Cited by 18
Linear Transformations Preserving the Real Orthogonal Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 561-572
-
- Article
-
- You have access
- Export citation
- Cited by 18
Thaine's Method for Circular Units and a Conjecture of Gross
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 302-317
-
- Article
-
- You have access
- Export citation


 almost everywhere with respect to Lebesgue measure on
almost everywhere with respect to Lebesgue measure on  almost everywhere
almost everywhere 
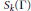

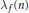
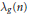

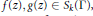
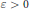
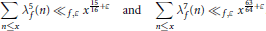
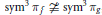
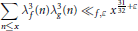
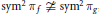
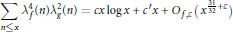
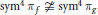
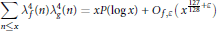
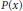
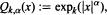
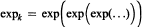 is the
is the 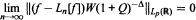

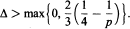

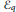
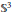
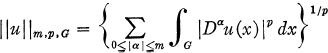


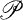 .
.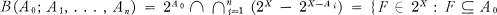 and
and 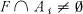 for all
for all 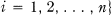 .
.