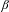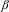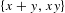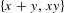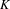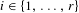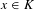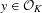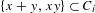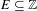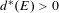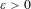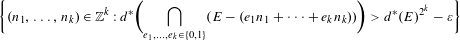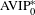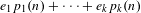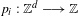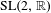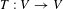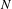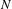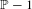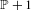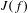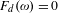Contents
Survey Article
Partial hyperbolicity and classification: a survey
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 401-443
-
- Article
- Export citation
Original Article
The Pisot conjecture for
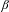 $\unicode[STIX]{x1D6FD}$ -substitutions
$\unicode[STIX]{x1D6FD}$ -substitutions
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 444-472
-
- Article
- Export citation
Measure preserving actions of affine semigroups and
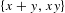 $\{x+y,xy\}$ patterns
$\{x+y,xy\}$ patterns
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 473-498
-
- Article
- Export citation
Sets of large values of correlation functions for polynomial cubic configurations
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 499-522
-
- Article
- Export citation
Discontinuity of Lyapunov exponents near fiber bunched cocycles
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 523-539
-
- Article
- Export citation
Entropy and its variational principle for locally compact metrizable systems
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 540-565
-
- Article
- Export citation
Syzygy sequences of the
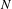 $N$ -center problem
$N$ -center problem
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 566-582
-
- Article
- Export citation
Invariant Jordan curves of Sierpiński carpet rational maps
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 583-600
-
- Article
- Export citation
Characterization of sets of limit measures of a cellular automaton iterated on a random configuration
-
- Published online by Cambridge University Press:
- 09 September 2016, pp. 601-650
-
- Article
- Export citation
Analogues of Auslander–Yorke theorems for multi-sensitivity
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 651-665
-
- Article
- Export citation
Closest integer polynomial multiple recurrence along shifted primes
-
- Published online by Cambridge University Press:
- 20 September 2016, pp. 666-685
-
- Article
- Export citation
On the measure-theoretic entropy and topological pressure of free semigroup actions
-
- Published online by Cambridge University Press:
- 26 July 2016, pp. 686-716
-
- Article
- Export citation
Physical measures for infinitely renormalizable Lorenz maps
-
- Published online by Cambridge University Press:
- 19 September 2016, pp. 717-738
-
- Article
- Export citation
The escaping set of transcendental self-maps of the punctured plane
-
- Published online by Cambridge University Press:
- 13 October 2016, pp. 739-760
-
- Article
- Export citation
Invariant circles and depinning transition
-
- Published online by Cambridge University Press:
- 22 September 2016, pp. 761-787
-
- Article
- Export citation
The generalized recurrent set and strong chain recurrence
-
- Published online by Cambridge University Press:
- 04 July 2016, pp. 788-800
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 38 Issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 15 March 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 38 Issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 15 March 2018, pp. b1-b2
-
- Article
-
- You have access
- Export citation