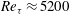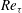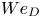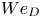Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Contents
Onsager's ‘ideal turbulence’ theory
-
- Published online by Cambridge University Press:
- 27 May 2024, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental and numerical investigation of turbulent spots in a flat plate boundary layer
-
- Published online by Cambridge University Press:
- 02 April 2025, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Defining the mean turbulent boundary layer thickness based on streamwise velocity skewness
-
- Published online by Cambridge University Press:
- 15 October 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis
-
- Published online by Cambridge University Press:
- 29 May 2018, pp. 821-867
-
- Article
-
- You have access
- HTML
- Export citation
Unsteady aerodynamic loads on pitching aerofoils represented by Gaussian body force distributions
-
- Published online by Cambridge University Press:
- 28 November 2025, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulation of turbulent channel flow up to
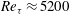 $\mathit{Re}_{{\it\tau}}\approx 5200$
$\mathit{Re}_{{\it\tau}}\approx 5200$
-
- Published online by Cambridge University Press:
- 10 June 2015, pp. 395-415
-
- Article
-
- You have access
- HTML
- Export citation
Water entry of cups and disks
-
- Published online by Cambridge University Press:
- 16 May 2023, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On deep-learning-based closures for algebraic surrogate models of turbulent flows
-
- Published online by Cambridge University Press:
- 08 October 2025, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Centre of mass location, flight modes, stability and dynamic modelling of gliders
-
- Published online by Cambridge University Press:
- 24 February 2022, A6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Taylor–Aris dispersion of active particles in oscillatory channel flows
-
- Published online by Cambridge University Press:
- 10 October 2025, A3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation