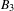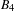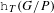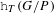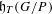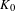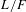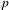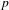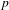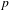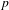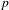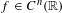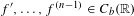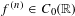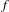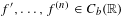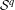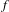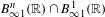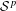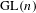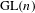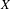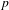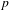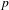Contents
Research Article
ANALOGUES OF CENTRALIZER SUBALGEBRAS FOR FIAT 2-CATEGORIES AND THEIR 2-REPRESENTATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1793-1829
-
- Article
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
-
- Article
- Export citation
ANALYTIC HYPOELLIPTICITY FOR SUMS OF SQUARES IN THE PRESENCE OF SYMPLECTIC NON TREVES STRATA
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1877-1888
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
-
- Article
- Export citation
TOWARDS A NON-ARCHIMEDEAN ANALYTIC ANALOG OF THE BASS–QUILLEN CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1931-1946
-
- Article
- Export citation
TWISTED TRIPLE PRODUCT
 $\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
$\text{p}$-ADIC L-FUNCTIONS AND HIRZEBRUCH–ZAGIER CYCLES
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2019, pp. 1947-1992
-
- Article
- Export citation
HIGHER ORDER DIFFERENTIABILITY OF OPERATOR FUNCTIONS IN SCHATTEN NORMS
- Part of:
-
- Published online by Cambridge University Press:
- 13 February 2019, pp. 1993-2016
-
- Article
- Export citation
PARITY OF THE LANGLANDS PARAMETERS OF CONJUGATE SELF-DUAL REPRESENTATIONS OF
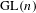 $\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
$\text{GL}(n)$ AND THE LOCAL JACQUET–LANGLANDS CORRESPONDENCE
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2019, pp. 2017-2043
-
- Article
- Export citation
WEIERSTRASS PRYM EIGENFORMS IN GENUS FOUR
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2019, pp. 2045-2085
-
- Article
- Export citation
LINEAR SYSTEMS ON IRREGULAR VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 12 March 2019, pp. 2087-2125
-
- Article
- Export citation
ON THE
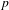 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 18 February 2019, pp. 2127-2164
-
- Article
- Export citation
THE KUGA–SATAKE CONSTRUCTION UNDER DEGENERATION
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 2165-2182
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 19 Issue 6 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 October 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 19 Issue 6 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 October 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation