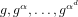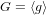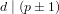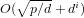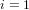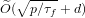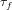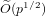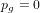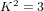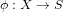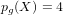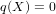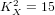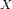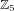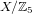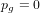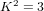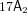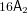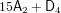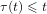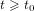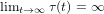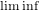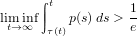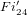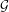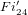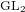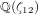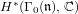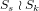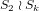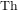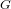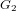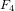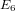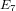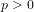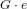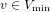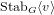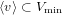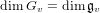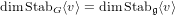Contents
Research Article
A new approach to the discrete logarithm problem with auxiliary inputs
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2016, pp. 1-15
-
- Article
-
- You have access
- Export citation
On the sum of the square of a prime and a square-free number
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2016, pp. 16-24
-
- Article
-
- You have access
- Export citation
A robust algorithm for estimating regression and dispersion parameters in non-stationary longitudinally correlated Com–Poisson data
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 25-36
-
- Article
-
- You have access
- Export citation
Zeroes of partial sums of the zeta-function
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2016, pp. 37-41
-
- Article
-
- You have access
- Export citation
Cuspidal quintics and surfaces with
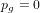 $p_{g}=0$ ,
$p_{g}=0$ , 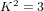 $K^{2}=3$ and 5-torsion
$K^{2}=3$ and 5-torsion
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2016, pp. 42-53
-
- Article
-
- You have access
- Export citation
Homaloidal nets and ideals of fat points I
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 54-77
-
- Article
-
- You have access
- Export citation
Computing cup products in integral cohomology ofHilbert schemes of points on K3 surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 78-97
-
- Article
-
- You have access
- Export citation
Oscillation of differential equations with non-monotone retarded arguments
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 98-104
-
- Article
-
- You have access
- Export citation
Structure of the
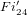 $Fi_{24}^{\prime }$ maximal
$Fi_{24}^{\prime }$ maximal  $2$ -local geometry point-line collinearity graph
$2$ -local geometry point-line collinearity graph
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2016, pp. 105-154
-
- Article
-
- You have access
- Export citation
Modular elliptic curves over the field of twelfth roots of unity
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 155-174
-
- Article
-
- You have access
- Export citation
A fourth-order seven-point cubature on regular hexagons
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 175-185
-
- Article
-
- You have access
- Export citation
Numerical semigroups with a given set of pseudo-Frobenius numbers
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 186-205
-
- Article
-
- You have access
- Export citation
The linear programming relaxation permutation symmetry group of an orthogonal array defining integer linear program
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 206-216
-
- Article
-
- You have access
- Export citation
An application of the
 $p$ -adic analytic class number formula
$p$ -adic analytic class number formula
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 217-228
-
- Article
-
- You have access
- Export citation
Finding 47:23 in the Baby Monster
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2016, pp. 229-234
-
- Article
-
- You have access
- Export citation
On the minimal modules for exceptional Lie algebras: Jordan blocks and stabilizers
- Part of:
-
- Published online by Cambridge University Press:
- 01 July 2016, pp. 235-258
-
- Article
-
- You have access
- Export citation
On a Li-type criterion for zero-free regions of certain Dirichlet series with real coefficients
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2016, pp. 259-280
-
- Article
-
- You have access
- Export citation
On the double Laplace transform of the truncated variation of a Brownian motion with drift
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2016, pp. 281-292
-
- Article
-
- You have access
- Export citation
Analysis of semilocal convergence for ameliorated super-Halley methods with less computation for inversion
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2016, pp. 293-302
-
- Article
-
- You have access
- Export citation