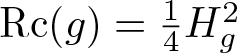Refine listing
Actions for selected content:
1419635 results in Open Access
INDEX
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 573-605
- Print publication:
- December 2024
-
- Article
- Export citation
APPENDIX 2 INVENTORY TAKEN AT BROOKE HOUSE, HOLBORN, 28 JULY 1643
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 509-519
- Print publication:
- December 2024
-
- Article
- Export citation
MAPS
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. ix-xi
- Print publication:
- December 2024
-
- Article
- Export citation
Is Intimate Partner Violence a Risk Factor for Alzheimer’s Disease?
-
- Journal:
- Canadian Journal of Neurological Sciences / Volume 52 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 737-738
-
- Article
- Export citation
Optimal mixing via tensorization for random independent sets on arbitrary trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 259-275
-
- Article
- Export citation
Generalized Ricci flow on aligned homogeneous spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 226-246
-
- Article
- Export citation
INTRODUCTION
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-32
- Print publication:
- December 2024
-
- Article
- Export citation
Widths of crossings in Poisson Boolean percolation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 26 November 2024, pp. 603-627
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACCOUNTS OF KATHERINE, LADY BROOKE, 1648–1649
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 447-502
- Print publication:
- December 2024
-
- Article
- Export citation
Quasi-steady transitions in confined convection
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 26 November 2024, A44
-
- Article
- Export citation
Beat the elite or concede defeat? Populist problem (re-)representations of international financial disputes
-
- Journal:
- Review of International Studies , First View
- Published online by Cambridge University Press:
- 26 November 2024, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ACCOUNTS OF MAJOR JOSEPH HAWKSWORTH, 1641–1643
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 233-320
- Print publication:
- December 2024
-
- Article
- Export citation
ACCOUNTS OF KATHERINE, LADY BROOKE, 1644–1645
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 343-369
- Print publication:
- December 2024
-
- Article
- Export citation
Homogeneous turbophoresis of heavy inertial particles in turbulent flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 999 / 25 November 2024
- Published online by Cambridge University Press:
- 26 November 2024, A83
-
- Article
- Export citation
Charmaine Robson, Missionary Women, Leprosy and Indigenous Australians, 1936-1986 (Cham: Palgrave Macmillan, 2022), pp. VIII + 265, £79.50, eBook, ISBN: 978-3-031-05796-0
-
- Journal:
- Medical History / Volume 68 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 488-489
-
- Article
-
- You have access
- HTML
- Export citation
ACCOUNTS OF MAJOR JOSEPH HAWKSWORTH, 1640–1641
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, pp. 187-232
- Print publication:
- December 2024
-
- Article
- Export citation
ABBREVIATIONS
-
- Journal:
- Royal Historical Society Camden Fifth Series / Volume 68 / December 2024
- Published online by Cambridge University Press:
- 26 November 2024, p. xv
- Print publication:
- December 2024
-
- Article
- Export citation
The Epistemic Fata Morgana: Appropriation in the Institutional Context
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lubrication-mediated rebounds off fluid baths
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 26 November 2024, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation