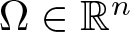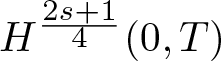Refine listing
Actions for selected content:
1419635 results in Open Access
When filth became dangerous: the miasmatic and contagionistic origins of nineteenth-century cleanliness practices among Swedish provincial doctors
-
- Journal:
- Medical History / Volume 69 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 22-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Richtmyer–Meshkov instability when a shock is reflected for fluids with arbitrary equation of state
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulation of turbulent flow and structures in a circular pipe subjected to axial system rotation
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quick-reference criteria for identifying multivariate cognitive change in older adults with mild cognitive impairment and dementia: An ADNI study
-
- Journal:
- Journal of the International Neuropsychological Society / Volume 30 / Issue 10 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 944-953
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enlargements and Morita contexts for rings with involution
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 131-162
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Impact of vaporization on drop aerobreakup
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Riemann–Hilbert problem and multiple high-order pole solutions to the cubic Camassa–Holm equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-51
-
- Article
- Export citation
Modelling turbulence in axisymmetric wakes: an application to wind turbine wakes
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics of projectable functions: towards an atlas of wandering domains for a family of Newton maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nuclearization on the Iberian Peninsula: A Tale of Two Countries (c. 1947–1988)
-
- Journal:
- Enterprise & Society / Volume 26 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 938-962
- Print publication:
- September 2025
-
- Article
- Export citation
DUAL NAKANO POSITIVITY AND SINGULAR NAKANO POSITIVITY OF DIRECT IMAGE SHEAVES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 55-78
- Print publication:
- March 2025
-
- Article
- Export citation
Natural convection in a vertical channel. Part 2. Oblique solutions and global bifurcations in a spanwise-extended domain
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Radial solutions of initial boundary value problems of nonlinear Schrödinger equations in ℝn
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mulder’s hail Mary
-
- Journal:
- Religious Studies / Volume 61 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 410-426
- Print publication:
- June 2025
-
- Article
- Export citation
Friction drag model for axial turbulent flow along the surface of a circular cylinder based on the universal characteristics of wall turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A35
-
- Article
- Export citation
On the transition in spanwise wake instability characteristics behind oscillating foils
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effect of random roughness on Stokes flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, R1
-
- Article
- Export citation
The unexpected impact of geographic access on take-up of social benefits
-
- Journal:
- Journal of Social Policy , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The fluid mechanics of spray cleaning: when the stress amplification at the contact lines of impacting droplets nano-scraps particles
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A31
-
- Article
- Export citation
Doing Business in the Public Interest
-
- Journal:
- Enterprise & Society / Volume 25 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 962-978
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation