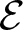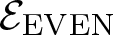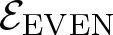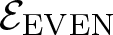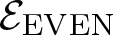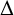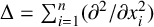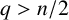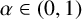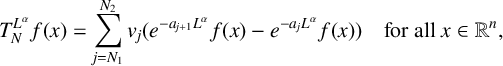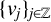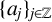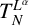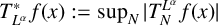Refine listing
Actions for selected content:
1419635 results in Open Access
JEH volume 84 issue 4 Cover and Front matter
-
- Journal:
- The Journal of Economic History / Volume 84 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. f1-f4
- Print publication:
- December 2024
-
- Article
-
- You have access
- Export citation
STATISTICAL ANALYSIS ON COMPLEXLY STRUCTURED DATA
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 184-185
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
Risk factors for healthcare-associated infection among patients hospitalized with COVID-19 infection
-
- Journal:
- Infection Control & Hospital Epidemiology / Volume 45 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1482-1483
- Print publication:
- December 2024
-
- Article
- Export citation
Sailing to Calanais: Monument Complexes and the Sea in the Neolithic of Western Scotland and Beyond
-
- Journal:
- Proceedings of the Prehistoric Society / Volume 90 / December 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 253-277
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The planar 3-colorable subgroup ε of Thompson’s group F and its even part
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 173-197
-
- Article
- Export citation
Destruction, delay and déjà vu: the restoration of Dublin’s O’Connell Street after the Irish civil war, 1922–1933
-
- Journal:
- Urban History / Volume 52 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 659-678
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combining internet-delivered cognitive behavioural therapy and attention bias modification for reducing depressive symptoms in firefighters: a randomized controlled trial
-
- Journal:
- Behavioural and Cognitive Psychotherapy / Volume 53 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 63-73
- Print publication:
- March 2025
-
- Article
- Export citation
Aging in a Changing World: Older New Zealanders and Contemporary Multiculturalism, Molly George, Rutgers University Press, New Brunswick, NJ, 2022, 192 pp., pbk $32.95, ISBN 13: 9781978809406
-
- Journal:
- Ageing & Society / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1034-1036
- Print publication:
- May 2025
-
- Article
- Export citation
Preserving large-scale features in simulations of elastic turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Christina Ramos, Bedlam in the New World: A Mexican Madhouse in the Age of Enlightenment (Chapel Hill: University of North Carolina Press, 2022), pp. xiv + 250, paperback, ISBN 978-146-9666-570.
-
- Journal:
- Medical History / Volume 68 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 25 November 2024, pp. 484-485
-
- Article
-
- You have access
- HTML
- Export citation
Existence of Bolgiano–Obukhov scaling in the bottom ocean?
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A38
-
- Article
- Export citation
Turbulent/turbulent entrainment in a planar wake
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pore-scale resolved direct numerical simulation study for scaling analysis of the solutal convection in porous media
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A21
-
- Article
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
- Export citation
Random growth via gradient flow aggregation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 735-755
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability evolution on a shock-accelerated cylindrical fluid layer with arbitrary Atwood numbers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A9
-
- Article
- Export citation
Uniqueness theorems for meromorphic inner functions and canonical systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 124-140
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Identification of cross-frequency interactions in compressible cavity flow using harmonic resolvent analysis
-
- Journal:
- Journal of Fluid Mechanics / Volume 1000 / 10 December 2024
- Published online by Cambridge University Press:
- 25 November 2024, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Navigating Diphtheria Resurgence in Pakistan’s Conflict-Ridden and Disaster-Prone Area
-
- Journal:
- Disaster Medicine and Public Health Preparedness / Volume 18 / 2024
- Published online by Cambridge University Press:
- 25 November 2024, e288
-
- Article
- Export citation