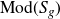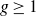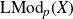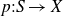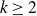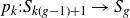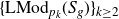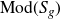Refine listing
Actions for selected content:
1416804 results in Open Access
Experiencing God in Late Medieval and Early Modern England. David J. Davis. Oxford: Oxford University Press, 2022. xiv + 226 pp. $105.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 274-276
- Print publication:
- Spring 2025
-
- Article
- Export citation
Actionism's Afterlife: Christoph Schlingensief Revisited
-
- Journal:
- Theatre Research International / Volume 50 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 13 March 2025, pp. 5-17
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mozart and/as AI
-
- Journal:
- Eighteenth-Century Music / Volume 22 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 March 2025, pp. 67-85
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Anna Nasiłowska. A History of Polish Literature. Trans. Anna Zaranko. Boston: Academic Studies Press, 2024. xvii, 682 pp. Bibliography. Index. $169.00, hard bound.
-
- Journal:
- Slavic Review / Volume 84 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 156-159
- Print publication:
- Spring 2025
-
- Article
- Export citation
TDR volume 69 issue 1 Cover and Back matter
-
- Journal:
- TDR: The Drama Review / Volume 69 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. b1-b6
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Fabien Carrié, Antoine Doré et Jérôme Michalon, Sociologie de la cause animale, Paris, La Découverte, 2023, 126 p.
-
- Journal:
- Annales. Histoire, Sciences Sociales / Volume 80 / Issue 1-2 / March 2025
- Published online by Cambridge University Press:
- 22 August 2025, pp. 430-433
- Print publication:
- March 2025
-
- Article
- Export citation
Bi-algebraic geometry of strata of differentials in genus zero
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 503-535
- Print publication:
- March 2025
-
- Article
- Export citation
A History of Emotion in Western Music: A Thousand Years from Chant to Pop Michael Spitzer New York: Oxford University Press, 2020 pp. xii + 456, ISBN 978 0 190 06175 3
-
- Journal:
- Eighteenth-Century Music / Volume 22 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 March 2025, pp. 121-124
- Print publication:
- March 2025
-
- Article
- Export citation
Nazi Volksgemeinschaft Technology: Gottfried Feder, Fritz Todt, and the Plassenburg Spirit By John C. Guse. Cham: Palgrave Macmillan, 2023. Pp. XXI, 309. Cloth GBP 109.99. ISBN 978-3-031-32055-2.
-
- Journal:
- Central European History / Volume 58 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 106-108
- Print publication:
- March 2025
-
- Article
- Export citation
LSR volume 59 issue 1 Cover and Back matter
-
- Journal:
- Law & Society Review / Volume 59 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 28 March 2025, pp. b1-b2
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Response to T.V. Paul’s Review of The New Experts: Populist Elites and Technocratic Promises in Modi’s India
-
- Journal:
- Perspectives on Politics / Volume 23 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 March 2025, pp. 345-346
- Print publication:
- March 2025
-
- Article
- Export citation
Leichte Klaviersonaten, Collections I and II Daniel Gottlob Türk (1750–1813), ed. Michael Tsalka and Angélica Minero Escobar Hong Kong: Artaria Editions, 2019 Collection I: pp. viii + 37, ISBN 978 9 88852 904 9 Collection II: viii + 38, ISBN 978 9 88852 906 3
-
- Journal:
- Eighteenth-Century Music / Volume 22 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 05 March 2025, pp. 137-140
- Print publication:
- March 2025
-
- Article
- Export citation
Xenia A. Cherkaev. Gleaning for Communism: The Soviet Socialist Household in Theory and Practice. Ithaca: Cornell University Press, 2023. xv, 189 pp. Notes. Bibliography. Index. Photographs. $125.00, hard bound. $26.95, paper.
-
- Journal:
- Slavic Review / Volume 84 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 229-230
- Print publication:
- Spring 2025
-
- Article
- Export citation
Government Use of Print: Official Publications in the Holy Roman Empire, 1500–1600. Saskia Limbach. Studien Zur Europäischen Rechtsgeschichte 326. Frankfurt: Vittorio Klostermann, 2021. xviii + 348 pp. €79.
-
- Journal:
- Renaissance Quarterly / Volume 78 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 18 June 2025, pp. 250-251
- Print publication:
- Spring 2025
-
- Article
- Export citation
Stuart Finkel. Revolutionary Philanthropy: Aid to Political Prisoners and Exiles in Late Imperial Russia. Oxford: Oxford University Press, 2024. xiii, 318 pp. Appendixes. Bibliography. Index. Maps. $115.00, hard bound.
-
- Journal:
- Slavic Review / Volume 84 / Issue 1 / Spring 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 223-224
- Print publication:
- Spring 2025
-
- Article
- Export citation
Response to MT Howard’s Review of Race and Diplomacy in Zimbabwe: The Cold War and Decolonization, 1960–1984.
-
- Journal:
- Perspectives on Politics / Volume 23 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 March 2025, p. 340
- Print publication:
- March 2025
-
- Article
- Export citation
JSL volume 90 issue 1 Cover and Front matter
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 10 April 2025, pp. f1-f3
- Print publication:
- March 2025
-
- Article
-
- You have access
- Export citation
Generating the liftable mapping class groups of regular cyclic covers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 157-176
- Print publication:
- March 2025
-
- Article
- Export citation
Authoritarian Practices in a Global Age. By Marlies Glasius. Oxford: Oxford University Press, 2023. 240p. $82.00 cloth. The Authoritarian International: Tracing How Authoritarian Regimes Learn in the Post-Soviet Space. By Stephen G. F. Hall. Cambridge: Cambridge University Press, 2023. 271p. $110.00 cloth. – CORRIGENDUM
-
- Journal:
- Perspectives on Politics / Volume 23 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 March 2025, p. 404
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
Cornell H Winston – President of AALL
-
- Journal:
- Legal Information Management / Volume 25 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 10 June 2025, pp. 3-7
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation