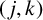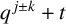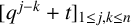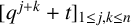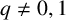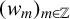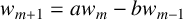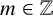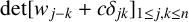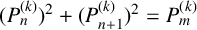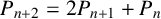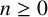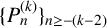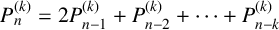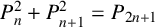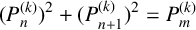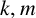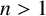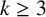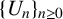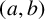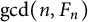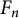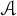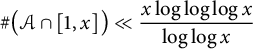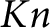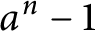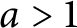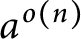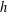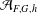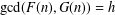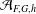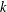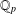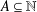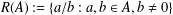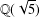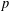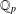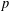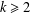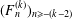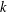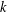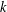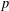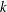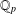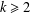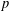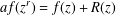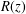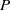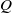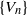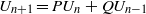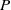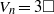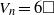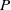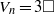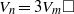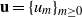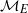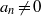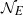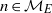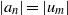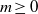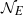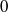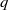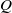Refine search
Actions for selected content:
21 results
Metallic mean Wang tiles II: the dynamics of an aperiodic computer chip
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 September 2025, e155
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Metallic mean Wang tiles I: self-similarity, aperiodicity and minimality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 August 2025, e133
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 227-236
- Print publication:
- October 2025
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
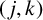 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 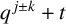 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
- Export citation
ON THE DIOPHANTINE EQUATION
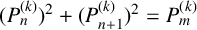 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 211-215
- Print publication:
- October 2024
-
- Article
- Export citation
A NOTE ON GENERALISED WALL–SUN–SUN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 373-378
- Print publication:
- December 2023
-
- Article
- Export citation
ON NEAR-PERFECT NUMBERS OF SPECIAL FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 366-372
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the greatest common divisor of n and the nth Fibonacci number, II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 617-625
- Print publication:
- June 2023
-
- Article
- Export citation
ALTERNATING CIRCULAR SUMS OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 385-395
- Print publication:
- December 2022
-
- Article
- Export citation
Terms of Lucas sequences having a large smooth divisor
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 225-231
- Print publication:
- March 2023
-
- Article
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation
ON NUMBERS
 $n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE
$n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE  $n$TH TERM OF A LINEAR RECURRENCE
$n$TH TERM OF A LINEAR RECURRENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 23-33
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
THE QUOTIENT SET OF
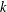 $k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN 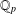 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 24-29
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 289-310
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
THE SQUARE TERMS IN GENERALIZED LUCAS SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 85-100
- Print publication:
- January 2014
-
- Article
- Export citation
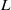 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
A linear recurrence sequence of composite numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 November 2012, pp. 360-373
-
- Article
-
- You have access
- Export citation
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ALGEBRAIC DIVISIBILITY SEQUENCES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 24 April 2012, pp. 99-126
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON SUMS OF FIBONACCI NUMBERS MODULO p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 17 November 2010, pp. 413-419
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation